Các câu hỏi tương tự
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w 2z + 1 - i là hình tròn có diện tích A. S 9π. B. S 12π. C. S 16π. D. S 25π.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích
A. S = 9π.
B. S = 12π.
C. S = 16π.
D. S = 25π.
Cho số phức z thỏa mãn:
z
z
¯
-
3
+
4
i
Tập hợp các điểm trong mặt phẳng Oxy biểu diễn các số phức z là:
Đọc tiếp
Cho số phức z thỏa mãn: z = z ¯ - 3 + 4 i Tập hợp các điểm trong mặt phẳng Oxy biểu diễn các số phức z là:
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z
-
(
3
-
4
i
)
2
A. Đường tròn tâm I(3;4) R12 B. Đường tròn tâm I(3;4) R4 C. Đường tròn tâm I(3;-4) R2 D. Đường tròn tâm I(3;...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện z - ( 3 - 4 i ) = 2
A. Đường tròn tâm I(3;4) R=12
B. Đường tròn tâm I(3;4) R=4
C. Đường tròn tâm I(3;-4) R=2
D. Đường tròn tâm I(3;4) R=8
Trong mặt phẳng Oxy, gọi M là điểm biểu diễn của số phức z3-4i và M là điểm biểu diễn của số phức . Diện tích của tam giác OMM bằng A.25/4 B.25/2 C.15/4 D.15/2
Đọc tiếp
Trong mặt phẳng Oxy, gọi M là điểm biểu diễn của số phức z=3-4i và M' là điểm biểu diễn của số phức ![]() . Diện tích của tam giác OMM' bằng
. Diện tích của tam giác OMM' bằng
A.25/4
B.25/2
C.15/4
D.15/2
Cho số phức z có biểu diễn hình học trong mặt phẳng tọa độ Oxy là điểm M(3;-4). Môđun của z bằng
A.25
B.5
C.1
D. 5
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2
(Đề thi Đại học năm 2009, khối D)
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2
(Đề thi Đại học năm 2009, khối D)
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
-
(
3
-
4
i
)
2
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - ( 3 - 4 i ) = 2
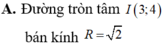
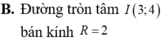
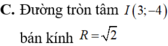
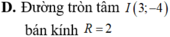
Cho số phức z thỏa mãn điều kiện
z
-
3
+
4
i
≤
2
. Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức
w
2
z
+
1
-
i
là hình tròn có diện tích
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 4 i ≤ 2 . Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức w = 2 z + 1 - i là hình tròn có diện tích
![]()
![]()
![]()
![]()




