Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Xét vị trí tương đối của mp x-2y-2z+1=0 và mặt cầu x^2+y^2 -2x+4y+8z-4=0
Vị trí tương đối của đường thẳng d: x = 2 + 4t, y = 3 + t, z = -5t và mặt phẳng (P): x + y + z - 3 = 0 là:
A. d ⊂ (P)
B. cắt nhau
C. song song
D. Đáp án khác
Đáp án C
Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là u d → = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là u p → = (1; 1; 1). Ta có:
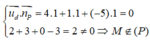
Suy ra đường thẳng d song song với mặt phẳng (P).
Cho hai điểm A(0;-1;2), B(4;1;-1) và mặt phẳng α : 3 x - y + z - 2 = 0 . Xét vị trí tương đối của hai điểm AB, và α .
A. A ∉ α , B ∈ α
B. A ∈ α , B ∉ α
C. A, B nằm về một phía đối với α
D. A, B nằm về hai phía đối với α
Đáp án D
Ta có f = 3 x - y + z - 2 ⇒ f A . f B = 1 . 8 = 8 > 0 ⇒ A, B nằm về hai phía đối với α .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d 1 : x = 1 y = 2 + t z = 2 − t và đường thẳng d 2 là giao tuyến của hai mặt phẳng P : x + y + z + 1 = 0 và Q : x − 2 y + z + 2 = 0 . Vị trí tương đối của hai đường thẳng d 1 , d 2 là
A. song song
B. cắt nhau.
C. chéo nhau.
D. trùng nhau.
Cho hai đường thẳng
∆ : x - 1 2 = y + 3 1 = z - 4 - 2 ∆ ' : x + 2 - 4 = y - 1 - 2 = z + 1 4
Xét vị trí tương đối giữa ∆ và ∆ ′
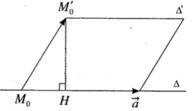
∆ đi qua điểm M 0 (1; -3; 4) và có vecto chỉ phương a → = (2; 1; −2)
∆ ′ đi qua điểm M 0 ’ (-2; 1; -1) và có vecto chỉ phương a → = (−4; −2; 4)
Ta có: 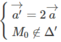
Vậy ∆ ′ song song với ∆
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x − y + z + 4 = 0 và mặt cầu S : x 2 + y − 1 2 + z − 3 2 = 12 . Khẳng định nào sau đây là đúng về vị trí tương đối của (P) và (S)?
A. Mặt phẳng (P) không cắt mặt cầu (S)
B. Mặt phẳng (P) tiếp xúc với mặt cầu (S)
C. Mặt phẳng (P) cắt mặt cầu (S)với giao tuyến là một đường tròn bán kính lớn nhất
D. Mặt phẳng (P) cắt mặt cầu (S)với giao tuyến là một đường tròn bán kính bằng 2 33
Trong không gian Oxyz, vị trí tương đối của hai đường thẳng :
d
1
: x = 2 + 4t, y = -6t, z = -1-8t và 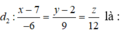
A. Cắt nhau
B. song song
C. chéo nhau
D. trùng nhau
Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
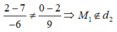
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.
Vị trí tương đối của đường thẳng 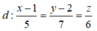 và mặt phẳng (P): x + y + z - 10 = 0 là:
và mặt phẳng (P): x + y + z - 10 = 0 là:
A. d ⊂ (P)
B. cắt nhau
C. song song
D. Đáp án khác
Đáp án B
Đường thẳng d đi qua A(1 ; 2 ; 0); có vecto chỉ phương là u d → (5; 7; 6)
Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1)
Ta có: u d → . n p → = 5.1 + 7.1 + 6.1 = 18
Suy ra: đường thẳng d cắt mặt phẳng (P).
Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 2 = y + 1 2 = z 3 ; ∆ 2 : x - 3 - 1 = y - 3 - 2 = z + 2 1
A. ∆ 1 song song với ∆ 2 .
B. ∆ 1 chéo với ∆ 2 .
C. ∆ 1 cắt ∆ 2 .
D. ∆ 1 trùng với ∆ 2 .
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau