Cho A, B, C là ba điểm trong mặt phẳng phức theo thứ tự biểu diễn các số: - 1 + i ; - 1 - i ; 2 i . Tính A B → . A C →
A. – 7.
B. 5.
C. – 2.
D. – 6.
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
![]()
![]()
![]()
![]()
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = − i ; z 2 = 2 + i ; z 3 = − 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành.
A. z = − 3 − i
B. z = − 2 − i
C. z = − 3
D. z = - 1 − 3 i
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i , z 2 = 2 + i , z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 – i
C. z = -1 – 3i
D. z = -3
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 - i
C. z = -1 - 3i
D. z = -3
Đáp án A
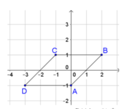
Ta có điểm A(0;-1), B(2;1), C(-1;1). Gọi D(a;b), khi đó ABCD là hình bình hành
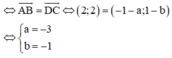
Suy ra số phức z biểu diễn D là z = -3 - i
Trên mặt phẳng tọa độ, các điểm A, B, C theo thứ tự biểu diễn các số phức 2+3i, 3+i, 1+2i.Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z
A. z=1+i
B.z=2+2i
C.z=2-2i
D.z=1-i
Trong mặt phẳng tọa độ xét ba điểm A, B, C theo thứ tự biểu diễn ba số phức z 1 , z 2 , z 3 thỏa mãn z 1 = z 2 = z 3 và z 1 + z 2 + z 3 = 0 . Hỏi tam giác ABC là tam giác gì?
A. Tam giác vuông cân
B. Tam giác vuông có một góc nhọn bằng 30°
C. Tam giác đều
D. Tam giác cân có góc ở đỉnh bằng 30°
Đáp án C.
Với bài toán này ta sẽ chọn trường hợp cụ thể thỏa mãn hai điều kiện trên, từ đó xét tam giác ABC là tam giác gì.
Chọn z 1 = 1 + 3 i ; z 2 = 1 − 3 i ; z 3 = − 2
⇒ A 1 ; 3 , B 1 ; − 3 , C − 2 ; 0 ⇒ A B = B C = C A = 2 3
Vậy ABC là tam giác đều.
Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức z 1 , z 2 khác 0 thỏa mãn đẳng thức z 1 2 + z 2 2 − z 1 z 2 = 0 , khi đó tam giác OAB (O là gốc tọa độ)
A. Là tam giác đều.
B. Là tam giác vuông.
C. Là tam giác cân, không đều.
D. Là tam giác tù.
Đáp án A.
Chọn z 1 = 1 ⇒ z 2 = 1 ± i 3 2 ⇒ z 2 − z 1 = − 1 ± i 3 2 .
Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức z 1 , z 2 khác 0 thỏa mãn đẳng thức z 1 2 + z 2 2 - z 1 z 2 = 0, khi đó tam giác OAB (O là gốc tọa độ)
A. Là tam giác đều.
B. Là tam giác vuông.
C. Là tam giác cân, không đều.
D. Là tam giác tù.
Đáp án A.
Cách 1: Ta có:
![]()
![]()
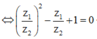
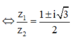
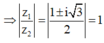
![]()
mặt khác 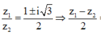
![]()
Do đó tam giác OAB là tam giác đều.
Cách 2: Chọn 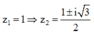
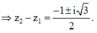
Trong mặt phẳng Oxy, gọi M, N theo thứ tự là các điểm biểu diễn cho số phức z và z ¯ (với z ≠ 0 ). Mệnh đề nào dưới đây đúng?
A.M và Nđối xứng với nhau qua trục Ox
B.M và N đối xứng với nhau qua trục Oy.
C. M và N đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất.
D.M và N đối xứng với nhau qua đường phân giác của góc phần tư thứ hai.