Tìm tập nghiệm S của phương trình log3( 2x+1) – log3(x-1) = 1
A.S= {4}
B. S= {3}
C. S= {-2}
D. S = {3}
Những câu hỏi liên quan
Tìm tập nghiệm S của phương trình log 3 ( 2 x + 1 ) - log 3 ( x - 1 ) = 1
A. S = {4}
B. S = {3}
C. S = {-2}
D. S = {1}
Tìm tập nghiệm S của phương trình:
log
3
2
x
+
1
-
log
3
-
1
1
. A.
S
3
B.
S
1
C.
S...
Đọc tiếp
Tìm tập nghiệm S của phương trình: log 3 2 x + 1 - log 3 - 1 = 1 .
A. S = 3
B. S = 1
C. S = 2
D. S = 4
ĐKXĐ: x > 1
Ta có:
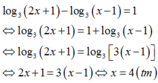
Vậy tập nghiệm S của phƣơng trình là: . S = 4
Chọn: D
Đúng 0
Bình luận (0)
Biết tập nghiệm S của bất phương trình log3( 9x-2) 1 là khoảng (a; b) . Tính hiệu số b- a A. b- a log910 B. b- a 1 C. D. 5
Đọc tiếp
Biết tập nghiệm S của bất phương trình log3( 9x-2) < 1 là khoảng (a; b) . Tính hiệu số b- a
A. b- a= log910
B. b- a= 1
C. 
D. 5
Tìm tập nghiệm của bất phương trình
log
3
(
2
x
-
3
)
1
A.
(
1
;
+
∞
)
B.
(
1
6
;
+
∞
)
C.
(
2
;
+
∞
)
D.
(
3
;
+
∞
)
Đọc tiếp
Tìm tập nghiệm của bất phương trình log 3 ( 2 x - 3 ) > 1
A. ( 1 ; + ∞ )
B. ( 1 6 ; + ∞ )
C. ( 2 ; + ∞ )
D. ( 3 ; + ∞ )
Tìm số nghiệm của phương trình l o g 3 ( x - 1 ) 2 + l o g 3 ( 2 x - 1 ) = 2
A. 0
B. 3
C. 1
D. 2
Tập nghiệm của phương trình
log
3
(
2
x
+
1
)
+
2
log
9
(
x
-
1
)
3
là A. {4}. B. {-7/2;4}. C...
Đọc tiếp
Tập nghiệm của phương trình log 3 ( 2 x + 1 ) + 2 log 9 ( x - 1 ) = 3 là
A. {4}.
B. {-7/2;4}.
C.{10}.
D. {2;10}.
Tìm tập nghiệm của phương trình
l
o
g
3
(
2
x
2
+
x
+
3
)
1
. A.
0
;
-
1
2
B.
0
C.
-
1
2...
Đọc tiếp
Tìm tập nghiệm của phương trình l o g 3 ( 2 x 2 + x + 3 ) = 1 .
A. 0 ; - 1 2
B. 0
C. - 1 2
D. 0 ; 1 2
Câu 1: [1] Gọi S là tập nghiệm của phương trình ( x+2)(2x-1)(x-3) = 0. Khẳng định nào sau đây sai?
A. -2 ∈ S B. 3 ∈ S C. 2 ∈ S D. \(\dfrac{1}{2}\) ∈ S
Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C
Đúng 2
Bình luận (0)
Phương trình
log
3
(
x
2
-
6
)
log
3
(
x
-
3
)
+
1
có tập nghiệm là: A.
T
∅
B. T {0;3} C. T {3} D. T {1;3}
Đọc tiếp
Phương trình log 3 ( x 2 - 6 ) = log 3 ( x - 3 ) + 1 có tập nghiệm là:
A. T = ∅
B. T = {0;3}
C. T = {3}
D. T = {1;3}
