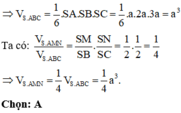
Cho hình chóp S.ABC có SA =2a, SB = 3a, SC = 4a và A S B = B S C = 60 0 , A S C = 90 0 . Tính thể tích V của khối chóp S.ABC
A. V = 2 a 3 2 9
B. V = 2 a 3 2
C. V = 4 a 3 2 3
D. V = a 3 2
Những câu hỏi liên quan
Cho hình chóp S.ABC có
S
A
2
a
,
S
B
3
a
,
S
C
4
a
và
∠
A
S
B
∠
B
S
C
60
°
,
∠
A
S
C
90
°
. Tính thể tích V của khối chóp S.ABC A. ...
Đọc tiếp
Cho hình chóp S.ABC có S A = 2 a , S B = 3 a , S C = 4 a và ∠ A S B = ∠ B S C = 60 ° , ∠ A S C = 90 ° . Tính thể tích V của khối chóp S.ABC
A. V = a 3 2
B. V = 4 a 3 2 3
C. V = 2 a 3 2
D. V = 2 a 3 2 9
Cho hình chóp S.ABC có SA 2a,
S
B
3
a
, SC 4a và
A
S
B
^
B
S
C
^
60
0
,
A
S
C
^...
Đọc tiếp
Cho hình chóp S.ABC có SA =2a, S B = 3 a , SC = 4a và A S B ^ = B S C ^ = 60 0 , A S C ^ = 90 0 . Tính thể tích V của khối chóp S.ABC.
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA a, SB 2a, SC 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là A.
5
a
6
B.
6
a
7
C.
7
a
6
D.
6...
Đọc tiếp
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 5 a 6
B. 6 a 7
C. 7 a 6
D. 6 a 5
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng
60
°
,
S
A
a
,
S
B
2
a
,
S
C
3
a
. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC) A.
a
3
B.
a
6
C.
a
6
3...
Đọc tiếp
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 60 ° , S A = a , S B = 2 a , S C = 3 a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
A. a 3
B. a 6
C. a 6 3
D. a 3 3
Chọn C.
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
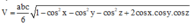
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc, biết SA 3a; SB 2a và thể tích của khối chóp S.ABC bằng a3. Tính độ dài SC. A.
S
C
a
6
B.
S
C
a
2
C.
S
C
a
D.
S
C
a
3
Đọc tiếp
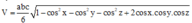
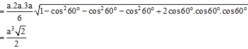
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc, biết SA = 3a; SB = 2a và thể tích của khối chóp S.ABC bằng a3. Tính độ dài SC.
A. S C = a 6
B. S C = a 2
C. S C = a
D. S C = a 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và
S
A
3
a
,
S
B
4
a
và
A
C
3
17
. Thể tích của khối chóp S.ABC bằng A.
24
a
3
B.
6
17
a
3
C.
48
a...
Đọc tiếp
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và S A = 3 a , S B = 4 a và A C = 3 17 . Thể tích của khối chóp S.ABC bằng
A. 24 a 3
B. 6 17 a 3
C. 48 a 3
D. 72 a 3
Cho khối chóp S.ABC có
A
S
B
^
B
S
C
^
C
S
A
^
60
°
,SAa,SB2a,SC4a. Tính thể tích khối chóp S.ABC theo a A.
8
a
3...
Đọc tiếp
Cho khối chóp S.ABC có A S B ^ = B S C ^ = C S A ^ = 60 ° ,SA=a,SB=2a,SC=4a. Tính thể tích khối chóp S.ABC theo a
A. 8 a 3 2 3
B. 2 a 3 2 3
C. 4 a 3 2 3
D. a 3 2 3
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 600, SA a, SB 2a, SC 3a. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
Đọc tiếp
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 600, SA = a, SB = 2a, SC = 3a. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và
S
A
a
,
S
B
2
a
,
S
C
3
a
. Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Tính theo a thể tích hình chóp S.AMN. A.
a
3
4
.
B.
3
a...
Đọc tiếp
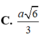
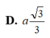
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và S A = a , S B = 2 a , S C = 3 a . Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Tính theo a thể tích hình chóp S.AMN.
A. a 3 4 .
B. 3 a 3 4 .
C. a 3 2 .
D. a 3
Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S
Đúng 0
Bình luận (0)