Biết rằng tồn tại hai giá trị của m sao cho hàm số y = x 3 - 3 x 2 + m đạt giá trị nhỏ nhất bằng 2 trên đoạn [-2;3]. Tính tổng hai giá trị đó, được kết quả là:
A. 18
B. 24
C. 20
D. 22
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
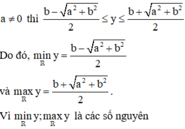
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
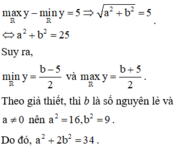
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
a)Cho hàm số y=ax+b. Tìm a và b biết rằng đồ thị của hàm số đã cho song song với đường thẳng 2x+y=3 và đi qua điểm M(2; 5).
b) Cho hai hàm số bậc nhất: y=(m-2)x+m và y=(m+3)x-m. Tìm giá trị của m để đồ thị của các hàm số cắt nhau tại một điểm trên trục tung?
Ta có: 2x+y=3 \(\Leftrightarrow\) y=-2x-3
a) Vì hs y=ax+b song song với đt y=-2x-3 nên\(\hept{\begin{cases}a=-2\\b\ne-3\end{cases}}\)
Suy ra pt y = ax + b là y = -2x + b (b\(\ne\)-3)
Mặt khác đt này lại đi qua điểm M(2;5) nên khi x=2 thì y=5. Ta có phương trình:
-2.2+b=5 \(\Leftrightarrow\)-4+b=5 \(\Leftrightarrow\) b=9
Vậy.......
Cho hàm số y = f(x) có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của hàm số m để phương trình f sin x = m có đúng hai nghiệm trên đoạn 0 ; π ?
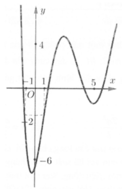
A. 4
B. 7
C. 5
D. 6
Biết rằng đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng d : y = - x + m tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất
A. m = 1
B. m = 2 3
C. m = 4
D. m = 0
Biết rằng đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng d:y=-x+m tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án DPhương trình hoành độ gaio điểm của đồ thị (C) và đường thẳng 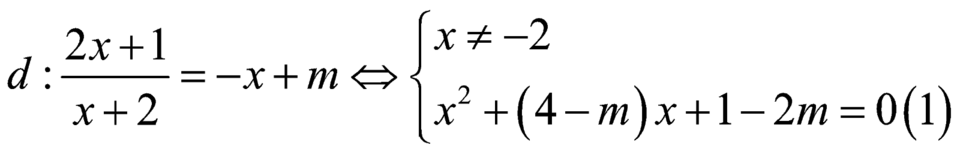
Gọi ![]() . Ta tính được
. Ta tính được ![]() khi m = 0
khi m = 0
Cho hàm số ( C m ) : y = x 3 - 5 x 2 + ( m + 4 ) x - m . Giá trị m để trên ( C m ) tồn tại ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng y = 1 2 x + 3 là
A. m ≤ 7 3
B. m ≥ 5 6
C. m ≥ 3
D. m ≤ 2
Cho hàm số y= 2 x + 1 1 3 + m 2 + m (m là tham số). Biết rằng có hai giá trị m 1 ; m 2 để giá trị lớn nhất của hàm số y=f(x) trên đoạn 7 12 ; 13 bằng 8. Tính .
A. T=9
B. T=4
C. T=36
D. T=25
cho hàm số y=x2 có đồ thị là (p)
1 tính giá trị của hàm số tại x=1/2;x=- căn 2
2 tìm x biết hàm số có giá trị bằng 9
3 xác định m để đường thẳng (Đ)y=2x-m cắt(P) tại hai điểm phân biệt a;b thỏa mãn 2Xa+Yb=5