Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số y = x 4 - 2 m x 2 + 1 đồng biến trên khoảng 2 ; + ∞ . Tổng giá trị các phần tử của T là
A. 8
B. 10
C. 4
D. 6
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
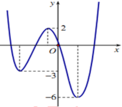
A. 12
B. 15
C. 18
D. 9
Hình vẽ bên là đồ thị của hàm số y = f(x). Gọi S là tập hợp các số nguyên dương của tham số m để hàm số y = |f(x – 1) + m| có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
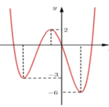
A. 12
B. 15
C. 18
D. 9
Đáp án A.
Phương pháp: Suy ra cách vẽ của đồ thị hàm số y = |f(x – 1) + m| và thử các trường hợp và đếm số cực trị của đồ thị hàm số. Một điểm được gọi là cực trị của hàm số nếu tại đó hàm số liên tục và đổi chiều.
Cách giải: Đồ thị hàm số y = f(x – 1) nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x) sang phải 1 đơn vị nên không làm thay đổi tung độ các điểm cực trị
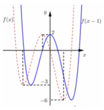
Đồ thị hàm số y = f(x – 1) + m nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x – 1) lên trên m đơn vị nên ta có: yCD = 2 + m; yCT = –3 + m; yCT = –6 + m
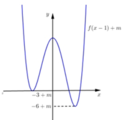
Đồ thị hàm số y = |f(x – 1) + m| nhận được bằng cách từ đồ thị hàm số y = f(x – 1) + m lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
Để đồ thị hàm số có 5 cực trị ![]()
![]()
=>S = {3;4;5} => 3+4+5 = 12
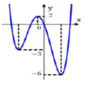
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
A. 9
B. 7
C. 12
D. 18
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số y = x - 2 x - m nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số y = x - 2 x - m nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
A. 2015
B. 2016
C. 2017
D. 2014
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
cho biểu thức f(x,y)= \(x^2+2y^2-2xy+2mx+2y+25\) ( m là tham số). Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để f(x,y) \(\ge\) 0 với x, y thuộc R. tính tổng tất cả các phần tử của S
\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)
Cho đồ thị của hàm số y = f x như hình vẽ dưới đây:
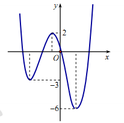
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 2017 + m có
5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập S bằng
A. 12
B. 15
C. 18
D. 9
Đáp án A
Nhận xét: Số giao điểm của C : y = f x với Ox bằng số giao điểm của C ' : y = f x − 2017 với Ox
Vì m > 0 nên C ' ' : y = f x − 2017 + m có được bằng cách tịnh tiến C ' : y = f x − 2017 lên trên m đơn vị
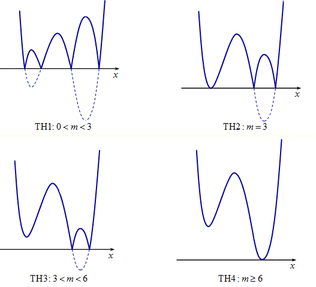
T H 1 : 0 < m < 3 Đồ thị hàm số có 7 điểm cực trị (loại)
T H 2 : m = 3 Đồ thị hàm số có 5 điểm cực trị (NHẬN)
T H 3 : 3 < m < 6 Đồ thị hàm số có 5 điểm cực trị (NHẬN)
T H 4 : m > 6 Đồ thị hàm số có 3 điểm cực trị (loại)
Vậy 3 ≤ m < 6. Do m ∈ ℤ * nên m ∈ 3 ; 4 ; 5
Vậy tổng giá trị tất cả các phần tử của S bằng 12
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2