Tính tích các đơn thức sau và tìm bậc của đơn thức thu được: 4xy2 và (-3)/4 (x2 y)3

Những câu hỏi liên quan
Tính tích các đơn thức sau và tìm bậc của đơn thức thu được.
a) 4xy2 và -3/4 ( x2y)3 ;
b) 1/6x(2y3)2 và -9x5y.
Bài 2: Tính tích các đơn thức sau và tìm bậc của đơn thức thu được:a, và b, ; và c, ; và Bài 3: Tính giá trị của các đơn thức sau:a, tại x -1, b, tại x -2, y 1c, tại x -6, y -1, a là hằng số
Đọc tiếp
Bài 2: Tính tích các đơn thức sau và tìm bậc của đơn thức thu được:
a, và
b,
;
và
c, ;
và
Bài 3: Tính giá trị của các đơn thức sau:
a, tại x = -1,
b, tại x = -2, y = 1
c, tại x = -6, y = -1, a là hằng số
\(2,\\ a,=-3x^3y^3z^4\\ b,=\dfrac{1}{4}xy^2\cdot\dfrac{1}{4}x^4y^4\cdot\left(-\dfrac{4}{5}yz^2\right)=-\dfrac{1}{20}x^5y^7z^2\\ c,=-\dfrac{15}{14}x^6y^{11}z^{10}\\ 3,\\ a,=9\left(-1\right)\left(-\dfrac{1}{27}\right)=\dfrac{1}{3}\\ b,=-\dfrac{1}{5}\left(-8\right)=\dfrac{8}{5}\\ c,=\dfrac{4}{9}a\cdot36\left(-1\right)=-16a\)
Đúng 1
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được: - 1 3 x 2 y v à 2 x y 3
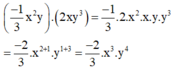
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.
Đúng 0
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
1 4 x 3 y v à - 2 x 3 y 5

Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12
Đúng 0
Bình luận (0)
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần bi...
Đọc tiếp
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A = 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B = 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C = 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D = 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần biến, tìm bậc của đơn thức. b) Tính giá trị của đơn thức C tại x= 1, y = -1 c) Tính giá trị của đơn thức D tại x = -1, y = -2 d) Chứng minh đơn thức C,D luôn nhận giá trị dương với mọi x ≠ 0, y ≠ 0, Bài 5. Cho A = 3xy – 4xy + 10xy – xy a) Tính giá trị của A tại x = 1, y = -1 b) Tìm điều kiện của x, y để A > 0. c) Tìm điều kiện của x, y để A > 0. d) Tìm x, y nguyên để A = - 24
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần bi...
Đọc tiếp
Bài 2: Thu gọn và tìm bậc của các đơn thức sau a) 2 5xy 2bx y ; b) 4 2 4 ab c 20a bx 5 ; c) 2 2 1 1,5xy bcx b 4 ; d) 2 3 2 2 1 2ax y x y zb 2 Bài 3: Cho biểu thức A = 2 3 𝑥 3 . 3 4 𝑥𝑦 2 . 𝑧 2 và B = 9x𝑦 3 . (−2𝑥 2𝑦𝑧 3 ) 1) Thu gọn và tìm bậc của đơn thức thu gọn A và B 2) Cho biết phần biến và phần hệ số của đơn thức thu gọn A và B 3) Tính tích của hai đơn thức thu gọn A và B. Bài 4:Cho đơn thức C = 2𝑥𝑦 2 ( 1 2 𝑥 2𝑦 2𝑥) ; D = 2 3 𝑥𝑦 2 . ( 3 2 𝑥) a) Thu gọn đơn thức C, D. Xác định phần hệ sô, phần biến, tìm bậc của đơn thức. b) Tính giá trị của đơn thức C tại x= 1, y = -1 c) Tính giá trị của đơn thức D tại x = -1, y = -2 d) Chứng minh đơn thức C,D luôn nhận giá trị dương với mọi x ≠ 0, y ≠ 0, Bài 5. Cho A = 3xy – 4xy + 10xy – xy a) Tính giá trị của A tại x = 1, y = -1 b) Tìm điều kiện của x, y để A > 0. c) Tìm điều kiện của x, y để A > 0. d) Tìm x, y nguyên để A = - 24
Tính tích các đơn thức sau và tìm bậc của đơn thức thu được: 1/6x(2y3)2 và -9x5y
1/6x(2y3)2.(-9.x5y)
= 1/6.x.4y6.(-9).x5.y
= [1/6.4.(-9)].(x.x5).(y6.y)
= -6.x6.y7
Đơn thức có bậc 6 + 7 = 13.
Đúng 0
Bình luận (0)
Tính tích các đơn thức sau và xác định phần hệ số, phần biến và tìm bậc của đơn thức thu được (
\(\left(-\dfrac{1}{4}x^2y^3\right)\left(\dfrac{6}{5}xy^2\right)\\ =\left(-\dfrac{1}{4}.\dfrac{6}{5}\right)\left(x^2.x\right)\left(y^3.y^2\right)\\ =-\dfrac{3}{10}x^3y^5\)
Hệ số: \(-\dfrac{3}{10}\)
Biến:x3y5
Bậc:8
Đúng 5
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
a) -\(\frac{1}{3}\)x2y và 2xy3;
b) \(\frac{1}{4}\)x3y và -2x3y5
(-\(\frac{1}{3}\)x2y) (2xy3) = (-\(\frac{1}{3}\) . 2) (x2 . x) (y . y3) = −23−23 x3 y4;
Đơn thức tích có bậc 7.
b) (\(\frac{1}{4}\)x3y) (-2x3y5) = - \(\frac{1}{2}\)x6 y6;
Đơn thức tích có bậc 12.
Đúng 0
Bình luận (0)













