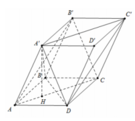
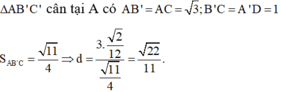Cho hình hộp thoi ABCD.A'B'C'D' có tất cả các cạnh bằng a và A B C ^ = B ′ B A ^ = B ′ B C ^ = 60 o . Chứng minh tứ giác A'B'CD là hình vuông.

Những câu hỏi liên quan
Cho hình hộp
A
B
C
D
.
A
B
C
D
có tất cả các mặt là hình thoi và các góc đỉnh A bằng
60
°
(tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng A. 17802. B. 15895. C. 14450. D. 16184.
Đọc tiếp
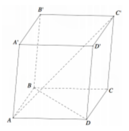
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60 ° (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
A. 17802.
B. 15895.
C. 14450.
D. 16184.
Cho hình hộp ABCD.ABCD có tất cả các mặt là hình thoi và các góc đỉnh A bằng
60
o
(tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng A.
90
o
B.
30
o
C.
45
o
D.
60...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60 o (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
A. 90 o
B. 30 o
C. 45 o
D. 60 o
Đáp án A
![]()
=>(ACC') là mặt phẳng trung trực của BD.
Do đó
![]()
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.ABCD có tất cả các mặt là hình thoi và các góc đỉnh A bằng
60
°
(tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng A. 90
°
B. 30
°
C. 45
°
D. 60
°
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60 ° (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng

A. 90 °
B. 30 °
C. 45 °
D. 60 °
Cho hình hộp
A
B
C
D
.
A
B
C
D
có tất cả các mặt là hình thoi và các góc đỉnh A bằng
60
°
(tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng A.
90
°
B.
30
°
C.
45
°
D.
60...
Đọc tiếp
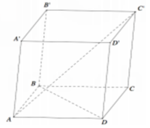
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60 ° (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
A. 90 °
B. 30 °
C. 45 °
D. 60 °
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau (hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B'D'
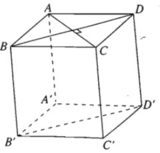
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD
Dễ thấy mặt chéo BDD'B' của hình hộp đã cho là hình bình hành, do đó BD // B′D′. Từ đó, theo bài 3.12 suy ra AC ⊥ B'D'.
Đúng 0
Bình luận (0)
Cho hình hộp \(ABCD.A'B'C'D'\) có độ dài tất cả các cạnh bằng \(a,AA' \bot (ABCD)\) và \(\widehat {BAD} = {60^0}\).
a) Tính thể tích của khối hộp \(ABCD.A'B'C'D'\).
b) Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {A'BD} \right)\).
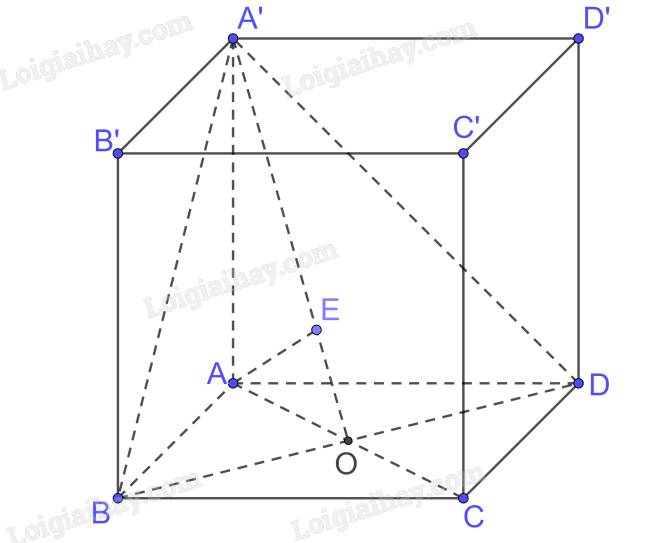
a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)
Diện tích tam giác ABD: \({S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích khối hộp là \(V = AA'.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
b) Gọi \(AC \cap BD = \left\{ O \right\}\)
Ta có \(AA' \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A'AO} \right);BD \subset \left( {A'BD} \right) \Rightarrow \left( {A'AO} \right) \bot \left( {A'BD} \right)\)
\(\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\)
Trong (A’AO) kẻ \(AE \bot A'O\)
\( \Rightarrow AE \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AE\)
Xét tam giác ABD có AB = AD và \(\widehat {BAD} = {60^0}\) nên tam giác ABD đều
\( \Rightarrow OA = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác AOA’ vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{{A'}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}\)
Vậy \(d\left( {A,\left( {A'BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\)
Đúng 0
Bình luận (0)
Cho hình hộp đứng
A
B
C
D
.
A
B
C
D
có tất cả các cạnh đều bằng a,
A
B
C
^
45
0
. Tính thể tích V của khối hộp
A
B
C
D
.
A
B
C
D...
Đọc tiếp
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng a, A B C ^ = 45 0 . Tính thể tích V của khối hộp A B C D . A ' B ' C ' D ' .
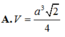
![]()
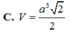
![]()
Cho hình hộp ABCD.ABCD có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
o
. Tính khoảng cách giữa hai đường thẳng AB và A C
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 o . Tính khoảng cách giữa hai đường thẳng AB' và A' C'
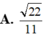
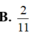
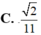
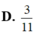
Cho hình hộp
A
B
C
D
.
A
B
C
D
có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
∘
. Tính khoảng cách giữa hai đường thẳng
A
B
v
à
A
C
A.
22
11
B. ...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ∘ . Tính khoảng cách giữa hai đường thẳng A B ' v à A ' C '
A. 22 11
B. 2 11
C. 2 11
D. 3 11
Đáp án A
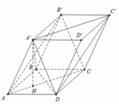
Do các góc phẳng đỉnh A đều bằng 60 ∘ và
nên các tam giác A ’ A D ; A ’ A B ; A B D là các tam giác đều cạnh 1.
Ta có:
A ' C ' / / A C ⇒ d A B ' ; A ' C ' = d A B ' C ; A ' C ' = d C ' ; A B ' C = 3 V C ' . A B ' C S . A B ' C
Mặt khác A ’ . A B D là hình tứ diện đều cạnh 1.
Ta có A H = 2 3 . A O = 3 3 ⇒ A ' H = A A ' 2 − A H 2 = 6 3 .
V = S A B C D = V A . C C ' B ' = 1 2 V A . C C ' B ' B = V 6 = 2 12
Δ A B ' C ' cân tại A có A B ' = A C = 3 ; B ' C = A ' D = 1
S A B ' C = 11 4 ⇒ d = 3. 2 12 11 4 = 22 11 .
Đúng 0
Bình luận (0)