Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 1 + x 1 - x

Những câu hỏi liên quan
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 3 x + 1
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 1 x - 2
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 4 x − x 2
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 3x − 5
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 4 x 2 − 0 , 6 x + 7
Sử dụng định nghĩa, tìm đạo hàm của các hàm số sau:
a) \(y = k{x^2} + c\) (với k, c là các hằng số);
b) \(y = {x^3}.\)
a) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k{x^2} + c - \left( {kx_0^2 + c} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {{x^2} - x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {x - {x_0}} \right)\left( {x + {x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left[ {k\left( {x + {x_0}} \right)} \right] = 2k{x_0}\)
Vậy hàm số \(y = k{x^2} + c\) có đạo hàm là hàm số \(y' = 2kx\)
b) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)
Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)
Đúng 0
Bình luận (0)
Bằng định nghĩa, tìm đạo hàm của hàm số sau y = 7 + x – x 2 tại x o = 1
Cách 1 : Áp dụng công thức
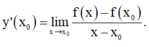

Cách 2 : Áp dụng công thức
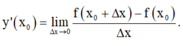

Đúng 0
Bình luận (0)
Bằng định nghĩa, tìm đạo hàm của hàm số sau: y = x 3 – 2 x + 1 tại x o = 2 .
Cách 1 : Áp dụng công thức
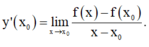
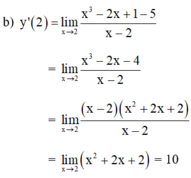
Cách 2 : Áp dụng công thức
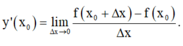
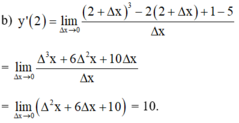
Đúng 0
Bình luận (0)
Sử dụng kết quả \(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1\), tính đạo hàm của hàm số \(y = {e^x}\) tại điểm x bất kì bằng định nghĩa
\(\begin{array}{l}f'(x) = \mathop {\lim }\limits_{x \to 0} \frac{{f(x + {x_0}) - f(x)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{x + {x_0}}} - {e^x}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{x + {x_0}}} - {e^x}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^x}({e^{{x_0}}} - 1)}}{x} = {e^x}.\mathop {\lim }\limits_{x \to 0} \frac{{{e^{{x_0}}} - 1}}{x} = {e^x}.1 = {e^x}\\ \Rightarrow f'(x) = {e^x}\end{array}\)
Đúng 0
Bình luận (0)






