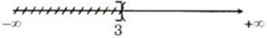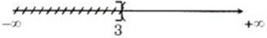Xác định các tập hợp sau: R \ (-∞; 3)

Những câu hỏi liên quan
Bài 4 xác định các tập hợp sau: a/ R\ (-1; + ∞ ) b/ R\ [0; 2)
R\(-1;+∞)=(-∞;-1]
R\[0;2)=(-∞;0)\(\cup\)[2;+∞)
Đúng 0
Bình luận (0)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (2; +∞)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (-∞; 3]
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (2; +∞)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (-∞; 3]
Xác định các tập hợp sau và biểu diễn chúng trên trục số
R \ (-1; 1)
R ( - 1 ; 1 ) = ( - ∞ - 1 ] ∪ [ 1 ; + ∞ )
Đúng 0
Bình luận (0)
Xác định các tập hợp sau và biểu diễn chúng trên trục số
R \ ((3; 5) ∩ (4; 6))
R ( ( 3 ; 5 ) ∩ ( 4 ; 6 ) ) = ( - ∞ ; 4 ) ∪ [ 5 ; + ∞ )
Đúng 0
Bình luận (0)
Xác định các tập hợp sau và biểu diễn chúng trên trục số
R \ ((0; 1) ∪ (2; 3))
R ( ( 0 ; 1 ) ∪ ( 2 ; 3 ) ) = ( - ∞ ; 0 ) ∪ [ 1 ; 2 ] ∪ [ 3 ; + ∞ )
Đúng 0
Bình luận (0)
Cho \(A = [-2;3],\;\,B = (1; + \infty )\). Xác định các tập hợp sau:
\(\;A \cap B; B \backslash A \) và \({C_\mathbb{R}}B\)
Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)
Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)
Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)
Đúng 0
Bình luận (0)