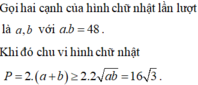Gọi độ dài một cạnh của hình chữ nhật là x (m) (điều kiện: x > 0).

⇒ độ dài cạnh còn lại : 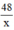 (m)

⇒ chu vi hình chữ nhật :

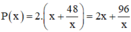
Xét hàm số 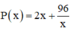 trên (0; +∞):

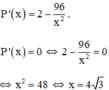
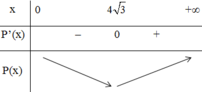
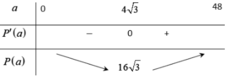
Bảng biến thiên trên (0; +∞):

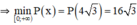
Vậy trong các hình chữ nhật có cùng diện tích 48 m 2  thì hình vuông cạnh 4 3 m có chu vi nhỏ nhất.

Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (x, y > 0). Khi đó xy = 48. Theo bất đẳng thức Cô-si, ta có :

. Vậy chu vi hình chữ nhật nhỏ nhất bằng (m) khi (m), tức là khi hình chữ nhật là hình vuông.

Gọi hai cạnh hình chữ nhật: \(x,y\left(x,y>0\right)\).
Do diện tích hình chữ nhật: \(xy=48\Rightarrow y=\dfrac{48}{x}\).
Chu vi hình chữ nhật là: \(2\left(x+y\right)=2\left(x+\dfrac{48}{x}\right)=\dfrac{2\left(x^2+48\right)}{x}\).
Xét hàm số: \(y=\dfrac{2\left(x^2+48\right)}{x}\) với \(x\in\left(0;+\infty\right)\).
\(y'\left(x\right)=\dfrac{2\left(x^2-48\right)}{x^2}\)
\(y'\left(x\right)=0\)\(\Leftrightarrow x=4\sqrt{3}\).
Bảng biến thiên:

Từ bảng biến thiên ta ta thấy giá trị nhỏ nhất của \(y\left(x\right)=16\sqrt{3}\) với \(x_{GTNN}=4\sqrt{3}\).
Suy ra hình chữ nhật có chu vi nhỏ nhất khi \(x=y=4\sqrt{3}\).

Chọn A.

Cách 1

Gọi cạnh của hình chữ nhật: a, b; 0 < a, b ≤ 48

Ta có, diện tích hình chữ nhật là 48 nên:

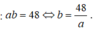
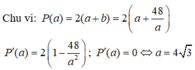
Bảng biến thiên:

Cách 2

+) Áp dụng bất đẳng thức Côsi:

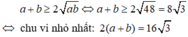
+) Hình chữ nhật có chu vi nhỏ nhất bằng  16 3   khi cạnh bằng  4 3

Đáp án là A

Đáp án C

Ta có S = a b = 48 P = 2 a + b ≥ 4 a b ⇔ a = b ⇔ a 2 = 48 ⇔ a = 48  

giúp mik với làm ơn

Áp dụng bất đẳng thức Co-si

Mà hình như đề bài thiếu dự kiện kìa cùng diện tích là bao nhiêu ????

Gọi độ dài của chiều dài và chiều rộng của hình chữ nhật lần lượt là a và b. (Điều kiện: a, b> 0)

Bài toán được diễn đạt lại là: "Cho a, b, < 0 và a.b = 100. Tìm giá trị nhỏ nhất của biểu thức a(a + b)"

Áp dụng bất đẳng thức Cô-si cho 2 số dương a và b, ta thu được chu vi nhỏ nhất bằng 40cm khi a = b = 10cm hay hình chữ nhật trở thành hình vuông

a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2)

Hình chữ nhật có kích thước là 1cm x 12cm có diện tích là 12cm2 và chu vi là (1 + 12).2 = 26 (cm) (có 26 > 15)

Hình chữ nhật kích thước 2cm x 7cm có diện tích là 14cm2 và chu vi là (2 + 7).2 = 18 (cm)

(có 18 > 15).

Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.

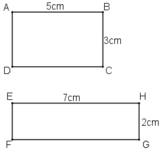
b) + Chu vi hình chữ nhật ABCD đã cho là (5 + 3).2 = 16 cm

Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là: 16 : 4 = 4 cm

Diện tích hình vuông này là 4.4 = 16 cm2

(Ở trên hình là ví dụ hình vuông MNPQ có cạnh là 4cm)

Vậy SHCN < SHV

+ Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Gọi cạnh của hình chữ nhật có độ dài lần lượt là a, b.

Hình vuông có cùng chu vi với hình chữ nhật nên cạnh hình vuông là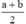 

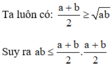
⇒ Hình vuông có diện tích lớn nhất.