Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
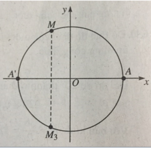
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Điều kiện để hàm số y=\frac{1+\cos x}{\sin x}y=sinx1+cosx xác định là
x\ne k\pi ,k\in ℤ.x=kπ,k∈Z.
x\ne -\pi +k2\pi ,k\in ℤ.x=−π+k2π,k∈Z.
x\ne \frac{\pi }{2}+k\pi ,k\in ℤ.x=2π+kπ,k∈Z.
x\ne \frac{\pi }{2}+k2\pi ,k\in ℤ.x=2π+k2π,k∈Z.
Bạn kiểm tra lại đề bài!
Hình như đề bài ko đúng đó bn!..bn kiểm tra lại
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
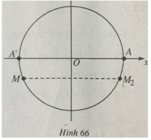
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
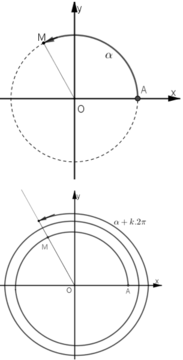
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Biểu diễn trên đường tròn lượng giác góc (cung) có số đo α:
a) α = 10350
b) α = 195π/3
c) α = π/2 + kπ, k∈Z
d) α = kπ
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Giá trị k để cung 
thỏa mãn 10π <
α
< 11
π
là
A. 4
B. 5
C. 6
D. 7
