Cho bốn cung (trên một đường tròn định hướng): ![]() Các cung nào có điểm cuối trùng nhau:
Các cung nào có điểm cuối trùng nhau:
A. α và β; γ và δ.
B. β và γ; α và δ.
C. α, β, γ.
D. β, γ, δ.
Cho bốn cung trên một đường tròn định hướng
\(\alpha=\dfrac{-5\pi}{6}\), \(\beta=\dfrac{\pi}{3}\)\(\gamma=\dfrac{25\pi}{3}\), \(\delta=\dfrac{19\pi}{6}\). Các cung nào có các điểm cuối trùng nhau. Giải thích rõ
Cho bốn cung (trên một đường tròn định hướng):
![]()
Các cung nào có điểm cuối trùng nhau:
Chọn B \(\beta\)và \(\gamma\) ;\(\alpha\)và \(\delta\)là các cặp góc lượng giác có điểm cuối trùng nhau.
Trên đường tròn lượng giác gốc A cho các cung có số đo:

Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ (I) và (II).
B. Chỉ (I), (II) và (III).
C. Chỉ (II), (III) và (IV).
D. Chỉ (I), (II) và (IV).
Chọn A.
Ta có: 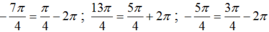
Suy ra chỉ có hai cung 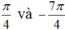 có điểm cuối trùng nhau.
có điểm cuối trùng nhau.
Trên đường tròn lượng giác gốc A. Cho các cung lượng giác có điểm đầu A và có số đo như sau:
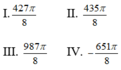
Các cung có điểm cuối trùng nhau là?
A. II và IV
B. I và II
C. I và III
D. I và IV
Đáp án: C
Ta có:

Vậy cung (I) và (III) có điểm cuối trùng nhau
Trên đường tròn đơn vị, gọi các điểm A, B, C, D lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho L, M, N, P lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút trùng với A và có số đo α = - 3 π 4 + k π . Mút cuối của trùng với điểm nào trong các điểm L, M, N, P?
A. L hoặc N
B. M hoặc P
C. M hoặc N
D. L hoặc P
Chọn A.

+ Vì L là điểm chính giữa 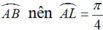
+ Vì N là điểm chính giữa 
+ Ta có 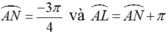
Vậy L hoặc N là mút cuối của 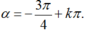
Trên đường tròn đơn vị, gọi các điểm A, B, A’, B’ lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho M, N, P, Q lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút là A và mút cuối trùng với một trong bốn điểm M, N, P, Q. Số do của là
A. α = 300+ k.3600
B. α= 600+ k.3600
![]()
![]()
Chọn D.
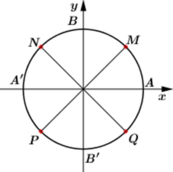
+ Ta có số đo cung ![]()
+ Ta có ![]()
+ Để mút cuối cùng trùng với một trong bốn điểm M; N; P; Q thì chu kì của cung α là ![]()
Vậy số đo cung ![]()
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra?
Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.
Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra ?
Trường hợp này xảy ra khi chúng sai khác nhau bội của 3600 (hay bội của 2π)
Cho đường tròn (O; R) và dây cung B C = R 3 cố định. Điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn. Gọi E là điểm đối ứng với B qua AC và F và điểm đối ứng với C qua AB. Các đường tròn ngoại tiếp các tam giác ABE và ACF cắt nhau tại K (K không trùng A). Gọi H là giao điểm của BE và CF.
c) Chứng minh AK luôn đi qua một điểm cố định
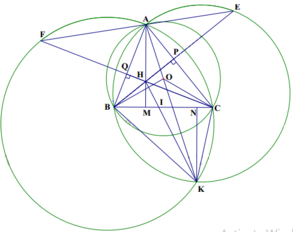
Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA