Cho góc α thỏa mãn tanα = 2. Tính P = 2 sin 2 α + 3 sin α . cos α + 4 cos 2 α 5 sin 2 α + 6 cos 2 α
A. P = 9 13
B. P = 9 65
C. P = 12 13
D. P = 8 13
Những câu hỏi liên quan
Cho góc α thỏa mãn tanα 2. Tính giá trị biểu thức
P
1
+
cos
α
+
cos
2
α
sin
α
+
sin
2
α
A. P...
Đọc tiếp
Cho góc α thỏa mãn tanα = 2. Tính giá trị biểu thức P = 1 + cos α + cos 2 α sin α + sin 2 α
A. P = 4
B. P = 1/2
C. P = 1
D. P = 1/4
Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn tanα 2 và 1800 α 2700 . Tính P cosα + sinα
Đọc tiếp
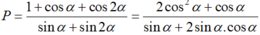
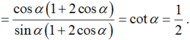
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
Cho góc α thỏa mãn tanα 2. Tính
P
3
sin
α
-
2
cos
α
5
cos
α
+
7
sin
α
A. P -4/9 B. P 4/9 C. P -4/19 D. P 4/19
Đọc tiếp
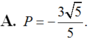
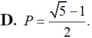
Cho góc α thỏa mãn tanα = 2. Tính P = 3 sin α - 2 cos α 5 cos α + 7 sin α
A. P = -4/9
B. P = 4/9
C. P = -4/19
D. P = 4/19
Chọn D.
Chia cả tử và mẫu của biểu thức P cho cosα ta được
Đúng 0
Bình luận (0)
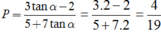
Cho góc α thỏa mãn tanα = 5. Tính P= sin4 α - cos4 α
A. P = 2
B. P = 1/2
C. P = 11/13
D. P = 12/13
Chọn D.
Ta có P = ( sin2α - cos2α) ( sin2α + cos2α) = sin2α - cos2α (*)
Chia hai vế của (*) cho cos2 α ta được 
Tương đương: P(1 + tan2α) = tan2α - 1
Đúng 0
Bình luận (0)
Cho góc
α
thỏa mãn
π
α
3
π
2
và
tan
α
2
: Tính giá trị của biểu thức
A
sin
2
α
+
cos
α
+
π
2
A.
4
+
2
5
10...
Đọc tiếp
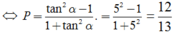
Cho góc α thỏa mãn π < α < 3 π 2 và tan α = 2 : Tính giá trị của biểu thức A = sin 2 α + cos α + π 2
A. 4 + 2 5 10
B. 4 + 5 5 5
C. 4 + 2 5 5
D. 2 + 5 5
Cho góc α thỏa mãn
cos
α
-
5
3
và
π
α
3
π
2
.Tính tanα.
Đọc tiếp
Cho góc α thỏa mãn cos α = - 5 3 và π < α < 3 π 2 .Tính tanα.
Cho góc α thỏa mãn
π
2
α
π
và tan α – cotα 1. Tính P tanα + cotα A. P 1 B. P -1 C.
P
-
5
D.
P
5
Đọc tiếp
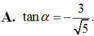
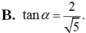
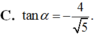
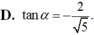
Cho góc α thỏa mãn π 2 < α < π và tan α – cotα = 1. Tính P = tanα + cotα
A. P = 1
B. P = -1
C. P = - 5
D. P = 5
Chọn C.
Ta có tan α – cotα = 1
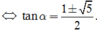
Do 
suy ra tanα < 0 nên
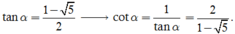
Thay
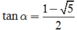và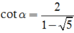 
vào P ta được
Đúng 0
Bình luận (0)
Cho góc
α
thỏa mãn điều kiện
π
α
3
π
2
và
tanα
2
Tính giá trị của biểu thức M
sin
2
α
+
sin
α
+
π
2
+...
Đọc tiếp
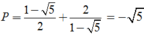
Cho góc α thỏa mãn điều kiện
π < α < 3 π 2 và tanα = 2
Tính giá trị của biểu thức M= sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α
Cho góc
α
thỏa mãn điều kiện
π
α
3
π
2
và
tan
α
2
. Tính giá trị của biểu thức
M
sin
2
α
+
sin
α
+
π...
Đọc tiếp
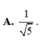
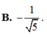
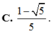
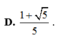
Cho góc α thỏa mãn điều kiện π < α < 3 π 2 và tan α = 2 . Tính giá trị của biểu thức
M = sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α
A. 1 5
B. - 1 5
C. 1 - 5 5
D. 1 + 5 5
Ta có
1 cos 2 α = 1 + tan 2 α = 1 + 4 = 5
Vì π < α < 3 π 2 nên cos α < 0
Suy ra cos α = 1 5
Khi đó
M = sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α
= sin 2 α + cos α + cos 2 α = sin 2 α + cos α + 2 cos 2 α - 1 = cos 2 α + cos α = 1 5 - 1 5 = 1 - 5 5
Đáp án C
Đúng 0
Bình luận (0)