Cho hình vẽ biết AM//CN. Chứng minh: ABC = A + C
Cho tam giác ABC vuông tại C . Biết B=2 góc A . Tính A và B a, Trên tia đôi tia CB lấy điểm D sao cho CD=CB . Chứng minh AD=AB b, Trên AD lấy điểm M , trên CD lấy điểm N sao cho AM = AN . Chứng minh CN = CM c, Chứng minh MN song song với BD TRÌNH BÀY CÁCH LÀM VÀ VẼ HÌNH NHA
A^ + B^ = 90o (phụ nhau)
A^ + 2* A^=90o
3* A^ = 90o
A^= 30o
B^= 2* A^ =2* 30o = 60o
a)
Xét \(\Delta\)ACD và \(\Delta\)ACB:
ACD^ = ACB^= 90o
AC chung
CD =CB
=> \(\Delta\)ACD =\(\Delta\)ACB (2 cạnh góc vuông)
=> AD = AB(2 cạnh tương ứng)
Phải là :Trên AD lấy M, trên AB lấy N (AM = AN) chứ.
b)
\(\Delta\)ACD =\(\Delta\)ACB (cmt) => A1 =A2 (2 góc tương ứng)
Xét \(\Delta\)AMC và \(\Delta\)ANC:
AC chung
A1 =A2 (cmt)
AM =AN
=> \(\Delta\)AMC = \(\Delta\)ANC (c.g.c)
=> CM =CN (2 cạnh tương ứng)
c)
AD = AB (cmt) =. D^ = B^
D^ + B^ + DAB^ =180o
2* D^ +DAB^=180o
D^= \(\frac{180o-DAB}{2}\) (1)
Ta có: AM = AN => AMN^ = ANM^
AMN^ + ANM^ + DAB^ =180o
2* AMN^ + DAB = 180o
AMN^ = \(\frac{180o-DAB}{2}\) (2)
Từ (1) và (2) => D^ = AMN^
Mà D^ so le trong với AMN^ => MN // DB
Cho hình vẽ biết AB = CD . Chứng minh Am= MB=CN=ND
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND
Cho tam giác ABC vuông tại C . Biết B=2 góc A . Tính A và B
a, Trên tia đôi tia CB lấy điểm D sao cho CD=CB . Chứng minh AD=AB
b, Trên AD lấy điểm M , trên CD lấy điểm N sao cho AM = AN . Chứng minh CN = CM
c, Chứng minh MN song song với BD
TRÌNH BÀY CÁCH LÀM VÀ VẼ HÌNH NHA
Cho tam giác ABC vuông tại C . Biết B=2 góc A . Tính A và B
a, Trên tia đôi tia CB lấy điểm D sao cho CD=CB . Chứng minh AD=AB
b, Trên AD lấy điểm M , trên CD lấy điểm N sao cho AM = AN . Chứng minh CN = CM
c, Chứng minh MN song song với BD
TRÌNH BÀY CÁCH LÀM VÀ VẼ HÌNH NHA
cho tam giác abc vuông cân tại a, đường cao ah và m là trung điểm ac.
a) chứng minh hm // ab và hm= ab:2
b) vẽ cn vuông góc với bm tại n. gọi d là giao điểm của hai đường thẳng ab và cn. chứng minh tứ giác admh là hình bình hành
c) chứng minh ad=am
a: ΔABC vuông cân tại A có AH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có CH/CB=CM/CA=1/2
nên HM//AB và HM/AB=CH/CB=1/2
=>HM=1/2AB
c: Xét ΔCDB có
CA,BN là đường cao
CA cắt BN tại M
=>M là trực tâm
=>DM vuông góc BC
=>góc MDB=90-45=45 độ
Xét ΔADM vuông tại A có góc ADM=45 độ
nên ΔADM vuông cân tại A
=>AD=AM
cho tam giác abc cân A BM và CN là các đường trung tuyến . Chứng minh a) BM = CN
b) AM= AN
Giúp mik vs ..Kèm hình vẽ nha
cho tam giác ABC cân tại A.Kẻ trung tuyến AM.a/ chứng minh AM là đương phân giác của tam giác ABC.b/tính AM biết AB=13cm và BC=10cm.c/qua M vẽ MN//AC(N thuộc AC).chứng minh:MN là đường trung tuyến của tam giác AMB.d/nối CN cắt AM tại G. chứng minh AM+CN>3/2AC
Cho hình vẽ sau, biết BM = CN . Chứng minh rằng góc ABC=góc ACB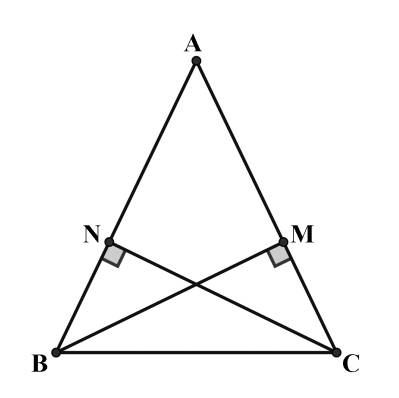
- Xét △BNC và △CMB có:
\(\widehat{BNC}=\widehat{CMB}=90^0\)
\(CN=BM\left(gt\right)\)
\(BC\) chung
⇒ △BNC = △CMB (ch - cgv)
⇒ \(\widehat{ABC}=\widehat{ACB}\left(đpcm\right)\)
Cho tam giác ABC cân tại A. Vẽ BM và CN là 2 đường trung tuyến. a/ Chứng minh: BM = CN b/Chứng minh: Tứ giác BNMC là hình thang cân. c/ Gọi I là giao điểm của BM và CN. Chứng minh: AI vuông góc với MN