Cho tam giác DEF có DE < DF. Đường cao DH
b. Lấy M ∈ DH. So sánh ME và MF
Những câu hỏi liên quan
Cho tam giác DEF có DE<DF .Vẽ đường cao DH
a,so sánh HE và HF
b,lấy điểm M trên DH,so sánh ME và MF
c,so sánh góc HDE và góc HDF
MỌI NGƯỜI GIÚP MÌNH NHA!
Khó vãi!!! Nghỉ ở nhà bây giờ ko nhớ tí kiến thức gì lun!!! Chắc phải mơ sách giáo khoa ra rùi tự nghiên cứu lại thui!!!
B. Phần tự luận (7 điểm)
Cho tam giác DEF có DE < DF. Đường cao DH
a. So sánh HE và HF
a. Vì DE < DF ⇒ HE < HF(quan hệ giữa hình chiếu và đường xiên) (1 điểm)
Đúng 0
Bình luận (0)
cho tam giác DEFcó DE<DF.Vẽ đường cao DH
a/So sánh HE và HF
b/Trên DH lấy điểm M.So sánh ME và MF.
bài này dựa vào quan hệ giữa đường xiên và hình chiếu nhé
Đúng 0
Bình luận (0)
Câu 1:Cho tam giác DEF có DEDF. Vẽ đường cao DH.a, So sánh HE và HF. b, Lấy M trên DH. So sánh ME và MF.c, So sánh góc HDE và HDF.Câu 2:Cho tam giác ABC vuông tại A. BD là đường phân giác của góc B( D thuộc AC ), vẽ DE vuông góc với BC tại E. Gọi F là giao điểm của AB và DE. Chứng minh rằng:a, tam giác ABC tam giác EBD.b, BD là đường trung trực của AE.c Tam giác DCF cân.d , Khi tam giác ABC có góc B 60 độ và BC12cm. Tính DC.MÌNH CẢM ƠN CÁC BẠN NHIỀU MONG CÁC BẠN GIÚP ĐỠ ĐẾN CHIỀU THỨ BA MÌNH KIỂ...
Đọc tiếp
Câu 1:
Cho tam giác DEF có DE<DF. Vẽ đường cao DH.
a, So sánh HE và HF.
b, Lấy M trên DH. So sánh ME và MF.
c, So sánh góc HDE và HDF.
Câu 2:
Cho tam giác ABC vuông tại A. BD là đường phân giác của góc B( D thuộc AC ), vẽ DE vuông góc với BC tại E. Gọi F là giao điểm của AB và DE. Chứng minh rằng:
a, tam giác ABC= tam giác EBD.
b, BD là đường trung trực của AE.
c Tam giác DCF cân.
d , Khi tam giác ABC có góc B= 60 độ và BC=12cm. Tính DC.
MÌNH CẢM ƠN CÁC BẠN NHIỀU MONG CÁC BẠN GIÚP ĐỠ ĐẾN CHIỀU THỨ BA MÌNH KIỂM TRA RỒI ^^^..
Câu 1 :
Ta có: Có DH _l_ EF (gt)
=> H là hình chiếu của D
mà DE < DF (gt)
=> HE < HF (quan hệ đường xiên hình chiếu)
2. Vì HE < HF (từ 1)
=> ME < MF (quan hệ đx, hình chiếu)
3. Xét ΔDHEΔDHE và ΔDHFΔDHF có:
DH: chung
H1ˆ=H2ˆ=90o(gt)H1^=H2^=90o(gt)
nhưng HE < HF (từ 1)
=> HDEˆ<HDFˆHDE^<HDF^ (vì HDEˆHDE^ đối diện với HE; HDFˆHDF^ đối diện với HF)
Đúng 0
Bình luận (0)
Cho tam giác DEF có DE < DF. Vẽ đường cao DH.
So sánh HE và HF. Lấy M trên DH. So sánh ME và MF. So sánh góc HDE và góc HDF.
Xét ΔDEF có DE<DF
mà HE là hình chiếu của DE trên EF
và HF là hình chiếu của DF trên EF
nên HE<HF
Xét ΔMEF có
EH là hình chiếu của ME trên EF
FH là hình chiếu của MF trên EF
mà EH<FH
nên ME<MF
Đúng 0
Bình luận (0)
Cho tam giác DEF có EF = 10cm, DE=6cm, DF=8cm. DH vuông góc với F tại M a)CMR: Tam giác DEF vuông b)Tính DH, HE, HI c)Gọi I là trung điểm DF vẽ IM vuông góc với EF CMR: DE2=ME2-MF2
Cho tam giác DEF có DE=6cm, DF=8cm, EF=10cm. Vẽ tia phân giác của góc E cắt cạnh DF tại M. Trên cạnh EF lấy điểm N sao cho EN=ED. Đường thẳng NM cắt đường thẳng DE tại I.
a) Chứng minh tam giác DEF là tam giác vuông
b) MN vuông góc EF rồi so sánh DM và MF
c) Gọi P, Q lần lượt là trung điểm của DN và IF. Chứng minh 3 điểm P, M, Q thẳng hàng
a/ Vì EF2=DE2+DF2 (Pytago)
=> Tam giác DEF vuông tại D
Đúng 0
Bình luận (0)
Cho tam giác DEF có EF = 10cm, DE=6cm, DF=8cm. DH vuông góc với F tai M a)CMR: Tam giác DEF vuông b)Tính DH, HE, HI c)Gọi I là trung điểm DF vẽ IM vuông góc với EF CMR: DE2= ME2-MF2
Tam giác DEF có DE < DF. Gọi d là đường trung trực của EF. M là giao điểm của d với DF.
a) Chứng minh DM + ME = DF.
b) Lấy bất kì điểm P nằm trên đường thẳng d (P khác M). Chứng minh DP + PE > DF.
c) So sánh chu vi của hai tam giác DEM và DEP.
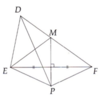
Do DE < DF nên M thuộc cạnh DF.
a) Có M thuộc đường trung trực của EF nên ME = MF
=> DM + ME = DM + MF = DF.
b) Vì P thuộc đường trung trực của EF nên PE = PF =>DP + PE = DP + PF.
Xét tam giác DEF: DP + PF > DF.
Vậy DE + PE > DF.
c) Từ ý a) và ý b) suy ra DP + PE > DM + ME.
Vậy chu vi tam giác DEP lớn hơn chu vi tam giác DEM.
Đúng 0
Bình luận (0)