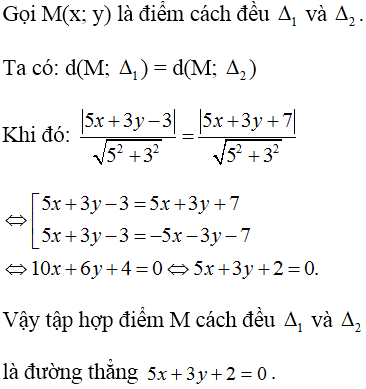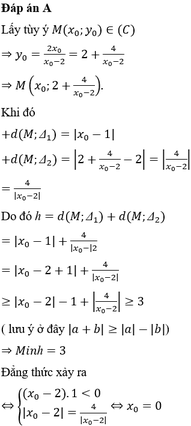Tìm tập hợp các điểm cách đều hai đường thẳng: (Δ1): 5x + 3y – 3 = 0 và (Δ2) : 5x + 3y + 7 = 0.

Những câu hỏi liên quan
Tìm tập hợp các điểm cách đều hai đường thẳng :
\(\Delta_1:5x+3y-3=0\)
\(\Delta_2:5x+3y+7=0\)
Tìm phương trình của tập hợp các điểm cách đều hai đường thẳng :
\(\Delta_1:5x+3y-3=0\)
\(\Delta_2:5x+3y+7=0\)
lời giải
\(\Delta_1\) //\(\Delta_2\)
Vậy \(\Delta_3\) cách đều phải //\(\Delta_2\) và \(\Delta_1\) và giữa \(\Delta_1\&\Delta_2\)
M(0,b)
x=0 =>\(\left\{{}\begin{matrix}\Delta_1=y=1\\\Delta_2\Rightarrow y=-\dfrac{7}{3}\end{matrix}\right.\)
=> b=\(\dfrac{\dfrac{3}{3}-\dfrac{7}{3}}{2}=\dfrac{-2}{3}\)
\(M=\left(0,-\dfrac{2}{3}\right)\)
\(\Delta_3\) phải đi qua M
=>\(\Delta_3\)=5x+3(y+2/3)=5x+3y+2=0
Đáp số: \(\Delta_3\)=5x+3y+2=0
Đúng 0
Bình luận (0)
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong trường hợp sau: Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
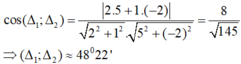
Đúng 1
Bình luận (0)
Góc giữa hai đường thẳng Δ1: 5x - y + 2 = 0 và Δ2: 3x + 2y + 1 = 0 là:
A. 30 °
B. 90 °
C. 45 °
D. 0 °
Chọn C.
Ta có:
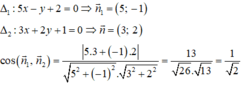
Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 ° .
Đúng 0
Bình luận (0)
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là:
A. 9x + 7y + 2 = 0 và 7x – 9y = 0
B. 9x – 7y + 2 = 0 và 77x – 99y + 46 = 0
C. 9x – 7y + 2 = 0 và 7x + 9y = 0
D. 9x + 7y + 2 = 0 và 77x – 99y + 46 = 0
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là hai đường phân giác ∆1,2 của chúng
Phương trình ∆1 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = 52 x − 39 y + 26 ⇔ − 27 x − 21 y − 6 = 0 ⇔ 9 x + 7 y + 2 = 0
Phương trình ∆2 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = − 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = − 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = − 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = − 52 x + 39 y − 26 ⇔ 77 x − 99 y + 46 = 0
Đáp án D
Đúng 0
Bình luận (0)
Tìm tập hợp các điểm cách 2 đường thẳng sau với tỉ lệ khoảng cách là \(\dfrac{5}{13}\)
- Cách 5 phần : (d) : 5x - 12y + 4 = 0
- Cách 13 phần: (Δ) : 4x - 3y - 10 = 0
Gọi \(M\left(x;y\right)\)
\(d\left(M,d\right)=\dfrac{5}{13}d\left(M,\Delta\right)\Leftrightarrow\dfrac{\left|5x-12y+4\right|}{13}=\dfrac{5}{13}.\dfrac{\left|4x-3y-10\right|}{5}\Leftrightarrow\left[{}\begin{matrix}x-9y+14=0\\9x-15y-6=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tập hợp các điểm cách 2 đường thẳng sau với tỉ lệ khoảng cách là \(\dfrac{5}{13}\)
- Cách 5 phần : (d) : 5x - 12y + 4 = 0
- Cách 13 phần: (Δ) : 4x - 3y - 10 = 0
Trong không gian Oxyz, tập hợp các điểm cách đều hai mặt phẳng (P): x + 3y - 4z + 1 0 và (Q): x + 3y - 4z + 7 0 là: A. x + 3y - 4z + 8 0 B. x + 3y - 4z + 6 0 C. x + 3y - 4z + 4 0 D. x + 3y - 4z - 6 0
Đọc tiếp
Trong không gian Oxyz, tập hợp các điểm cách đều hai mặt phẳng (P): x + 3y - 4z + 1 = 0 và (Q): x + 3y - 4z + 7 = 0 là:
A. x + 3y - 4z + 8 = 0
B. x + 3y - 4z + 6 = 0
C. x + 3y - 4z + 4 = 0
D. x + 3y - 4z - 6 = 0
Đáp án C
Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi
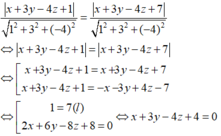
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
x
-
2
có đồ thị (C). Tìm giá trị nhỏ nhất h của tổng khoảng cách từ điểm M thuộc (C) tới hai đường thẳng
Δ
1
:
x
-
1
0
;
Δ
2
:
y
-
2
0
. A. h 4 B...
Đọc tiếp
Cho hàm số y = 2 x x - 2 có đồ thị (C). Tìm giá trị nhỏ nhất h của tổng khoảng cách từ điểm M thuộc (C) tới hai đường thẳng Δ 1 : x - 1 = 0 ; Δ 2 : y - 2 = 0 .
A. h = 4
B. h = 3
C. h = 5
D. h = 2