Cho tam giác ABC vuông tại A. M là trung điểm BC
A) c/m tam giác AMC cân
B) c/m tam giác AMB cân
Cho tam giác ABC vuông tại A. M là trung điểm BC
A ) c/m tam giác AMC cân
B) c/m tam giác AMB cân
Cho tam giác ABC cân tại A,M là trung điểm của BC a: chứng minh tam giác AMB= tam giác AMC b:qua A vẽ a vuông góc AM.Gọi N là giao điểm của 2 đường thẳng A và B. Chứng minh tam giác AMC=tam giác CNA
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
DO đó: ΔAMB=ΔAMC
b: Bổ sung đề: Qua C, kẻ đường thẳng b đi qua C và vuông góc với BC.
ΔAMB=ΔAMC
=>\(\hat{AMB}=\hat{AMC}\)
mà \(\hat{AMB}+\hat{AMC}=180^0\) (hai góc kề bù)
nên \(\hat{AMB}=\hat{AMC}=\frac{180^0}{2}=90^0\)
=>AM⊥BC
Ta có: AM⊥BC
CN⊥BC
DO đó: AM//CN
Ta có: AN⊥AM
BC⊥AM
DO đó; AN//CB
=>AN//CM
Xét ΔAMC vuông tại M và ΔCNA vuông tại N có
CA chung
\(\hat{MAC}=\hat{NCA}\) (hai góc so le trong, AM//CN)
Do đó: ΔAMC=ΔCNA
cho tam giác ABC cân tại A có M là trung điểm của BC
a) chứng minh tam giác AMB= tam giác AMC
b) vẽ đường thăng vuông góc với BC tại C cắt BA tại N. chứng minh tam giác ANC cân
c) gọi H là trung điểm của Nc, I là trung điểm của AC. chứng minh M,I,N thẳng hàng
cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC.
a) CM: tam giác AMB= tam giác AMC
b) CMR: đường thẳng AM là đường trung trực của BC.
c) CM: tam giác AMB vuông cân.
d) Tia phân giác góc ABC cắt AM tại I. Tính số đo góc BIC
e) CMR: IM+BC = nửa chu vi của tam giác ABC.
( CHỈ CẦN LÀM PHẦN e THÔI NHÉ )
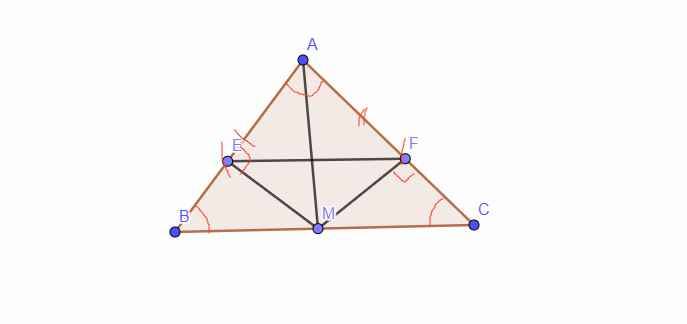
Cho tam giác ABC cân tại A, M là trung điểm của BC,a)chứng minh tam giác amb=tam giác amc b)Từ M kẻ các đường ME vuông góc với Ab(E ∈ AB); MF vuông góc với Ac (F ∈ AC). Chứng minh ea=fa c)chứng minh ef song song bc
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
bài này ko đúng phần b vs c giống đề bài bọn tôi
cho tam giác ABC cân tại A, M là trung điểm của BC. CMR: a, tam giác AMB= tam giác AMC. b, tính độ dài AM biết AB=10cm; BC=12cm c, kẻ đường trung tuyến CE cắt AM tại D. gọi I là điểm cách đều 3 cạnh của tam giác ABC. CMR: I;D;M thẳng hàng.
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
Cho tam giác ABC vuông tại A có góc B=60*
Gọi M là trung điểm của BC .
a) Chứng minh tam giác AMB đều và tam giác AMC cân
b) Vẽ MI vuông góc với AC tại I. C/M MI=1/2 AB
Cho tam giác ABC cân tại A có AB=AC=10cm, BC=12cm.
a)Gọi M là trung điểm của BC. C/minh tam giác AMB= tam giác AMC.
b) Tính AM.
c) Vẽ BK vuông góc AC, CF vuông góc AB. C/minh BK=CF và AK=AF.
CHO tam giác ABC cân tại A,M là trung điểm BC
a.chứng minh tam giác AMB=AMC
b.Vẽ ME vuông góc AB TẠI E ,MF vuông góc AC tại F.Chứng minh AM vuông góc AF
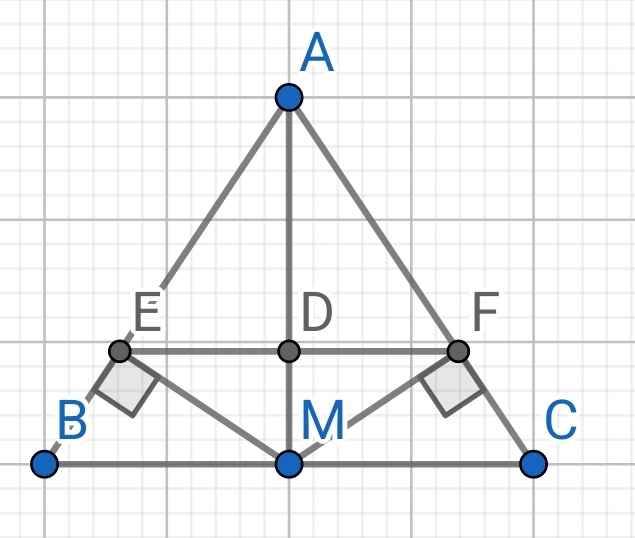 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = CM
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆AMB và ∆AMC có:
AM là cạnh chung
AB = AC (cmt)
BM = CM (cmt)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Sửa đề:
Chứng minh AM EF
Giải:
Gọi D là giao điểm của AM và EF
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAE = ∠MAF
Xét hai tam giác vuông: ∆MAE và ∆MAF có:
AM là cạnh chung
∠MAE = ∠MAF (cmt)
⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)
⇒ AE = AF (hai cạnh tương ứng)
Do ∠MAE = ∠MAF (cmt)
⇒ ∠DAE = ∠DAF
Xét ∆ADE và ∆ADF có:
AD là cạnh chung
∠DAE = ∠DAF (cmt)
AE = AF (cmt)
⇒ ∆ADE = ∆ADF (c-g-c)
⇒ ∠ADE = ∠ADF (hai góc tương ứng)
Mà ∠ADE + ∠ADF = 180⁰ (kề bù)
⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰
⇒ AD ⊥ EF