Phương trình nào sau đây là phương trình tham số của đường thẳng d: 2x- 6y + 23 0.
Đọc tiếp
Phương trình nào sau đây là phương trình tham số của đường thẳng d: 2x- 6y + 23= 0.
Những câu hỏi liên quan
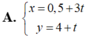
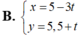
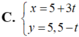
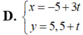
Cho đường thẳng (d) có phương trình tổng quát: 2x+ 6y - 8=0. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng (d) .
A. ( 2; 6)
B. (1; 3)
C. (4; -1)
D. ( 3; -1)
Đường thẳng đã cho có VTPT là n → ( 2; 6) nên có VTCP là u → ( 6; -2)
Mà vecto u 1 → ( 3; -1) cùng phương với vecto u → nên vecto này cũng là VTCP của đường thẳng đã cho..
Chọn D.
Đúng 0
Bình luận (0)
Cho đường thẳng ∆ có phương trình tổng quát là 2x – y – 2 0. Phương trình nào sau đây là phương trình tham số của ∆? A.
x
3
+
2
t
y
4
−
t
B....
Đọc tiếp
Cho đường thẳng ∆ có phương trình tổng quát là 2x – y – 2 = 0. Phương trình nào sau đây là phương trình tham số của ∆?
A. x = 3 + 2 t y = 4 − t
B. x = 1 + 2 t y = − 1 + 4 t
C. x = 3 + 4 t y = 1 − 2 t
D. x = 3 + t y = 4 + 2 t
ĐÁP ÁN D
Đường thẳng ∆ có vectơ pháp tuyến n → = 2 ; − 1 ⇒ ∆ có vectơ chỉ phương là u → = 1 ; 2 hoặc các vectơ khác vectơ – không mà cùng phương với nó.
Ta chỉ quan tâm đến phương án B và D. Kiểm tra tiếp hai điểm M 1 3 ; 4 , M 2 1 ; − 1 xem điểm nào nằm trên ∆. Ta có M 1 ∈ ∆ , M 2 ∉ ∆
Vậy phương trình tham số của đường thẳng ∆: x = 3 + t y = 4 + 2 t
Chú ý. Do phương trình tham số của đường thẳng là không duy nhất nên ta sẽ đi kiểm tra các phương án trả lời được đưa ra thay cho việc tiến hành viết phương trình tham số của đường thẳng.
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxyz, cho đường thẳng d:
x
-
1
1
y
-
2
-
2
z
+
2
3
. Phương trình nào sau đây là phương trình tham số của d?
Đọc tiếp
Trong hệ tọa độ Oxyz, cho đường thẳng d: x - 1 1 = y - 2 - 2 = z + 2 3 . Phương trình nào sau đây là phương trình tham số của d?
Trong hệ tọa độ Oxyz, cho đường thẳng
d
:
x
−
1
1
y
−
2
−
2
z
+
2
3
. Phương trình nào sau đây là phương trình tham số của d? A. ...
Đọc tiếp
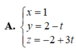
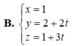
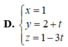
Trong hệ tọa độ Oxyz, cho đường thẳng d : x − 1 1 = y − 2 − 2 = z + 2 3 . Phương trình nào sau đây là phương trình tham số của d?
A. x = 1 y = 2 − t z = − 2 + 3 t
B. x = 1 y = 2 + 2 t z = 1 + 3 t
C. x = 1 + t y = 2 − 2 t z = − 2 + 3 t
D. x = 1 y = 2 + t z = 1 − 3 t
Phương trình nào sau đây là phương trình tham số của đường thẳng?
A. \(2x - y + 1 = 0\)
B. \(\left\{ \begin{array}{l}x = 2t\\y = t\end{array} \right.\)
C. \({x^2} + {y^2} = 1\)
D. \(y = 2x + 3\)
Phương trình nào sau đây là phương trình tham số của đường thẳng
d
:
x
5
-
y
7
1
Đọc tiếp
Phương trình nào sau đây là phương trình tham số của đường thẳng d : x 5 - y 7 = 1
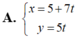
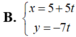
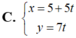
Đường thẳng d có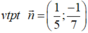 
, chọn 
và đi qua điểm M(5; 0)
Vậy phương trình tham số của đường thẳng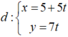 
.
Chọn C
Đúng 0
Bình luận (0)
Đường thẳng d có phương trình chính tắc
x
+
1
-
3
y
-
2
1
.Phương trình nào sau đây là phương trình tham số của d?
Đọc tiếp
Đường thẳng d có phương trình chính tắc x + 1 - 3 = y - 2 1 .Phương trình nào sau đây là phương trình tham số của d?
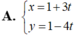
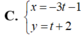
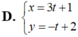
Đường thẳng d có 
và đi qua điểm M(-1; 2)
Vậy phương trình tham số của đường thẳng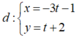 
.
Chọn C.
Đúng 0
Bình luận (0)
Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7 0 là: D.Tất cả sai
Đọc tiếp
Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7= 0 là:
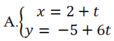
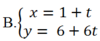
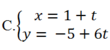
D.Tất cả sai
Đáp án A
Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.
Mà đường thẳng (d’) có VTPT là n → ( 1 ; 6 ) n ê n u → ( 1 ; 6 ) là VTCP của đường thẳng (d) .
Khi đó phương trình tham số của đường thẳng (d) cần tìm là:
Đúng 1
Bình luận (0)
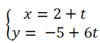
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0
Bình luận (0)