Cho hàm số f(x) xác định trên R\{1} bởi f ( x ) = 2 x x - 1 . Giá trị của bằng:
A. 1 2
B. - 1 2
C. -2
D. Không tồn tại
Những câu hỏi liên quan
Cho hàm số f(x) xác định trên R bởi f(x)= 2 x 2 + 1 . Giá trị f ' (-1) bằng:
A. 2
B. 6
C. - 4
D. 3
Chọn C
Ta có : .f ' (x)=4x ⇒ f ' (-1)=-4
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f’(-1) bằng:
A. 2.
B. 6.
C. -4.
D. 3.
Chọn C.
Ta có : f’(x) = 4x ⇒ f’(-1) = -4.
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên R bởi f ( x ) = 2 x 2 + 1 . Giá trị f'(-1) bằng:
A. 2
B. 6
C. -4
D. 3
Cho hàm số f(x) xác định trên R bởi
f
(
x
)
x
2
. Giá trị f (0) bằng A. 0 B. 2 C. 1 D. không tồn tại
Đọc tiếp
Cho hàm số f(x) xác định trên R bởi f ( x ) = x 2 . Giá trị f ' (0) bằng
A. 0
B. 2
C. 1
D. không tồn tại
Chọn D
Ta có : f ' x = 1 2 x 2 . ( x 2 ) ' = x x 2
-> f '(x) không xác định tại x = 0
-> f ' (0) không có đạo hàm tại x= 0
Đúng 0
Bình luận (0)
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra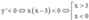 
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x)
x
(
x
2
-
1
)
(
x
-
4
)
,
∀
x
∈
R
. Hàm số
g
(
x
)
(
f
(
x
)
)
2
-
2
f...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x) = x ( x 2 - 1 ) ( x - 4 ) , ∀ x ∈ R . Hàm số g ( x ) = ( f ' ( x ) ) 2 - 2 f ( x ) f '' ( x ) đồng biến trên khoảng nào ?
A. (0;1).
B. (-1;0).
C. ( 4 ; + ∞ ) .
D. ( - ∞ ; - 1 ) .
Cho hàm số yf(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)(1-x)(x+2).g(x) + 2018 trong đó g(x)0, mọi x thuộc R. Hàm số yf(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thoả mãn f'(x) = (1 - x)(x+2)g(x) + 2023 với g(x) < 0, ∀x∈R. Hàm số y = f(1-x) + 2023x + 2024 nghịch biến trên khoảng nào?
Cho hàm số \(y = f(x)\) xác định trên \(R\) có đạo hàm \(f'(x)=-(x+2)(x-1)^2(x-3)\)
Số điểm cực tiểu của hàm số \(f(x^2-2x)\) là?
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
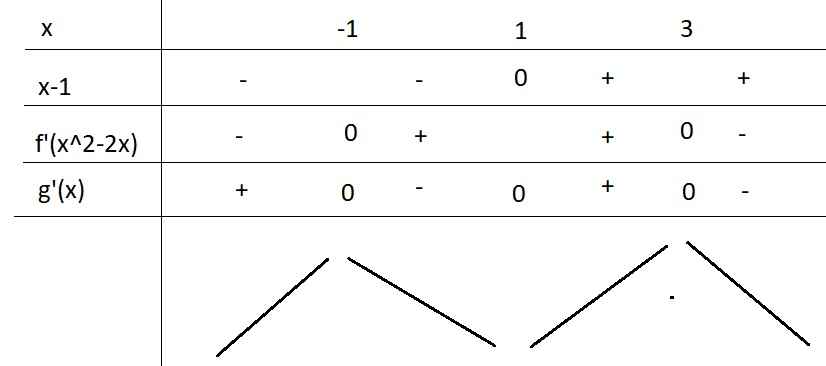
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu
Đúng 1
Bình luận (0)