Cho hình cầu (O;R) hai mặt phẳng (P) và (Q) song song với nhau, cách đều O, đồng thời cắt khối cầu thành ba phần sao cho thể tích phần nằm giữa hai mặt phẳng bằng 13 27 thể tích khối cầu .Tính khoảng cách giữa (P) và (Q).
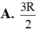
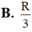
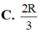

Một hình trụ có tâm các đáy là O,O′. Biết rằng mặt cầu đường kính OO′ tiếp xúc với các mặt đáy của hình trụ tại O,O′ và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 8π. Tính diện tích xung quanh của hình trụ đã cho.
A. 16 π
B. 8 π 3
C. 8 π
D. 16 π 3
Đáp án C
Theo bài ra ta có chiều cao của hình trụ bằng đường kính đáy của hình trụ và bằng đường kính của mặt cầu.
Gọi bán kính của mặt cầu là R

Một hình trụ có tâm các đáy là O, O’. Biết rằng mặt cầu đường kính OO’ tiếp xúc với các mặt đáy của hình trụ tại O, O’ và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 8 π . Tính diện tích xung quanh của hình trụ đã cho.
A. 8 π
B. 16 π
C. 8 π 3
D. 16 π 3
Đáp án A
Theo bài ra ta có chiều cao của hình trụ bằng đường kính đáy của hình trụ và bằng đường kính của mặt cầu.

Cho mặt cầu tâm O. Đường thẳng d cắt mặt cầu này tại hai điểm M, N. Biết rằng MN = 24 và khoảng cách từ O đến d bằng 5. Tính diện tích S của hình cầu đã cho
A. S = 100 π
B. S = 48 π
C. S = 52 π
D. S = 676 π
Đáp án D
Ta có:
R = d 2 + M N 2 2 = 25 + 12 2 = 13 ⇒ S = 4 π R 2 = 676 π .
1. Cho đường tròn (O). Trên đường tròn đó lấy ngẫu nhiên 3 điểm A, B, C. Tính xác suất để \(\Delta ABC\) chứa tâm O của đường tròn.
2. Cho hình cầu tâm (O). Trên mặt hình cầu lấy ngẫu nhiên 4 điểm A, B, C, D. Tính xác suất để hình tứ diện ABCD chứa tâm O của hình cầu.
1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)
Cho hình nón tròn xoay đáy là đường tròn (C) tâm O, bán kính R = 3 2 , đường cao SO = 3 2 . Xét hình cầu tâm I, nhận (O) làm đường tròn nhỏ và nhận tất cả đường sinh của hình nón làm tiếp tuyến. Tính thể tích hình cầu.
A. V = π 3
B. V = 2 π 3
C. V = 4 π 3
D. V = 5 π 3
Gọi ST là đường sinh hình nón
Ta có:
tan I S T ^ = 3 3 ⇒ O S T ^ = I S T ^ = 30 o
∆ O I T c ó R = O T cos 30 o = 3 2 . 2 3 = 1
Vậy V = 4 3 πR 3 = 4 π 3
Đáp án C
Cho hình nón tròn xoay đáy là đường tròn (C) tâm O, bán kính R = 3 2 , đường cao SO = 3 2 . Xét hình cầu tâm I, nhận (O) làm đường tròn nhỏ và nhận tất cả đường sinh của hình nón làm tiếp tuyến. Tính thể tích hình cầu.
A. V = π 3
B. V = 2 π 3
C. V = 4 π 3
D. V = 5 π 3
Cho hình vẽ bên gồm: • Hình cầu tâm O bán kính là OA. • Hình nón có đường cao là AI và đường kính đường tròn đáy là BC (B và C thuộc mặt cầu tâm O bán kính OA, I ∈ BC, O ∈ AI). Biết BAC= 60 độ , thể tích hình nón là Vnón = 24π (cm3 ). Tính bán kính và thể tích của hình cầu (kết quả làm tròn đến hàng đơn vị).
Cho khối cầu tâm O bán kính 6 cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng:
A. 2 cm.
B. 3 cm.
C. 4 cm.
D. 0 cm.

Ta có bán kính đường tròn đáy của hình nón ![]() , chiều cao khối nón h = 6 + x
, chiều cao khối nón h = 6 + x
Thể tích khối nón:

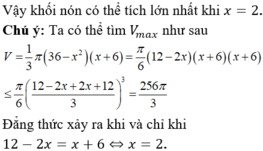
Cho khối cầu tâm O, bán kính 6cm. Mặt phẳng (P) cách O một khoảng h cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của h bằng
A. 2cm
B. 3cm
C. 4cm
D. 0cm
Đáp án A
Kí hiệu bán kính đáy của hình nón là x, chiều cao hình nón là y (trong đó 0<x≤2R; 0<y≤R). Gọi SS’là đường kính của mặt cầu ngoại tiếp hình nón thì ta có:
![]() (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Gọi V1 là thể tích khối nón: 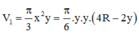
Mặt khác 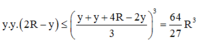
Do đó 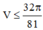 dấu bằng xảy ra
dấu bằng xảy ra ![]()
Khi đó 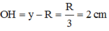
Cho khối cầu tâm O, bán kính 6cm. Mặt phẳng (P) cách O một khoảng h cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của h bằng
A. 2cm
B. 3cm
C. 4cm
D. 0cm