Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt
A. 6
B. 2
C. 3
D. 5
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Tính tổng tất cả các nghiệm thực của phương trình log 4 3 . 2 x - 1 = x - 1
A. -6
B. 5
C. 12
D. 2
Tính tổng tất cả các nghiệm thực của phương trình log 4 3.2 x − 1 = x − 1
A. - 6
B. 5
C. 12
D. 2
Tổng tất cả các nghiệm thực của phương trình log 6 3 . 4 x + 2 . 9 x = x + 1 bằng
A. 4
B. 1
C. 0
D. 3
Tổng tất cả các nghiệm của phương trình log5(6-5x)=1-x bằng
ĐKXĐ: \(6-5^x>0\Rightarrow5^x< 6\)
\(log_5\left(6-5^x\right)=1-x\Leftrightarrow6-5^x=5^{1-x}\)
\(\Leftrightarrow5^x-6+\frac{5}{5^x}=0\Leftrightarrow\left(5^x\right)^2-6.5^x+5=0\)
\(\Rightarrow\left[{}\begin{matrix}5^x=1\\5^x=5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\) \(\Rightarrow\sum x=0+1=1\)
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
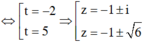
Vậy phương trình có các nghiệm: 
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
Tổng tất cả các nghiệm thực của phương trình 2 log 4 x - 3 + log 4 x - 5 2 = 0 là
