Cho số phức z a+bi ; a,b
∈
ℝ
. Nhận xét nào sau đây luôn đúng?
Đọc tiếp
Cho số phức z = a+bi ; a,b ∈ ℝ . Nhận xét nào sau đây luôn đúng?
Những câu hỏi liên quan
Cho số phức za+bi. Mô đun của số phức z bằng: A.
a
2
-
b
2
B.
a
2
+
b
2
C.
a
2
+
b
2
D.
a...
Đọc tiếp
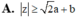
Cho số phức z=a+bi. Mô đun của số phức z bằng:
A. a 2 - b 2
B. a 2 + b 2
C. a 2 + b 2
D. a 2 - b 2
Cho hai số phức
z
a
+
b
i
và
z
a
+
b
i
. Tìm phần ảo của số phức zz
Đọc tiếp
Cho hai số phức z = a + b i và z ' = a ' + b ' i . Tìm phần ảo của số phức zz'
Cho hai số phức
z
a
+
b
i
và
z
’
a
’
+
b
’
i
. Tìm phần ảo của số phức zz’. A. aa’+bb’ B. ab’-a’b’ C. ab’+a’b D. aa’-bb’
Đọc tiếp
Cho hai số phức z = a + b i và z ’ = a ’ + b ’ i . Tìm phần ảo của số phức zz’.
A. aa’+bb’
B. ab’-a’b’
C. ab’+a’b
D. aa’-bb’
Cho số phức
z
a
+
b
i
khác 0. Số phức
z
-
1
có phần thực là A.
a
a
2
+
b
2
B.
-
b
a
2...
Đọc tiếp
Cho số phức z = a + b i khác 0. Số phức z - 1 có phần thực là
A. a a 2 + b 2
B. - b a 2 + b 2
C. a
D. 1 a 2 + b 2
Cho số phức
z
a
+
b
i
khác 0. Số phức
z
-
1
có phần thực là
Đọc tiếp
Cho số phức z = a + b i khác 0. Số phức z - 1 có phần thực là
Cho số phức
z
a
+
bi
.
Tìm điều kiện của a và b để số phức
z
2
(
a
+
bi
)
2
là số thuần ảo
A...
Đọc tiếp
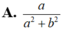
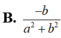
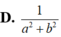
Cho số phức z = a + bi . Tìm điều kiện của a và b để số phức z 2 = ( a + bi ) 2 là số thuần ảo
A . a = 2 b .
B . a = 3 b .
C . a = ± b .
D . a ≠ 0 , b ≠ 0 .
Chọn C.
Ta có: z 2 = ( a + bi ) 2 = a 2 - b 2 + 2 abi . Để z 2 là số thuần ảo thì a 2 - b 2 = 0 ⇔ a = ± b .
Đúng 0
Bình luận (0)
Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Đúng 0
Bình luận (0)
Cho hai số phức
z
a
+
b
i
và
z
’
a
’
+
b
’
i
(a,b,a’,b’ÎR) . Số phức zz’ có phần thực là A. aa’ + bb’ B. ab’ – a’b C. aa’ - bb’ D. ab’ + a’b
Đọc tiếp
Cho hai số phức z = a + b i và z ’ = a ’ + b ’ i (a,b,a’,b’ÎR) . Số phức zz’ có phần thực là
A. aa’ + bb’
B. ab’ – a’b
C. aa’ - bb’
D. ab’ + a’b
Cho hai số phức:
z
a
+
b
i
,
z
a
+
b
i
(
a
,
b
,
a
,
b
∈
ℝ
)
.
Tìm phần ảo của số phức
z
z
. A....
Đọc tiếp
Cho hai số phức:
z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ ) .
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' − a ' b
D. a a ' − b b '
Đáp án A.
Có z . z ' = a a ' − b b ' + a b ' + a ' b i .
Vậy phần ảo là: a b ' + b a ' i .
Đúng 0
Bình luận (0)
Cho hai số phức
z
a
+
b
i
,
z
a
+
b
i
(
a
,
b
,
a...
Đọc tiếp
Cho hai số phức z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ )
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' - a ' b
D. a a ' - b b '
Đáp án A.
Có 
.
Vậy phần ảo là (ab'+ba')i.
Đúng 0
Bình luận (0)