Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô đậm như hình bên được giới hạn bởi một đồ thị hàm số bậc ba đa thức và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu?
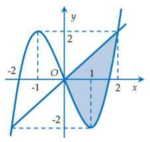
A. S = 8
B. S = 6
C. S = 2
D. S = 4
Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô đậm như hình bên được giới hạn bởi một đồ thị hàm số bậc ba đa thức và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu ?
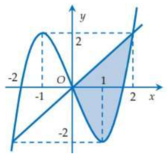
A. S = 8
B. S = 6
C. S = 2
D. S = 4
Đáp án D
Giả sử đồ thị hàm số có dạng y = ax 3 + b x 2 + c x + d
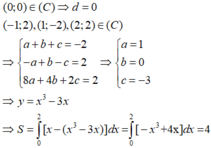
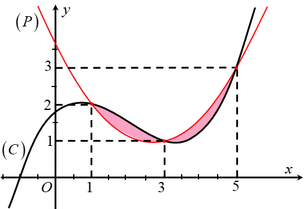
Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm số đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
A. 37 12
B. 7 12
C. 11 12
D. 5 12
Cho hàm số bậc hai y = f x = x 4 − 5 x 2 + 4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?
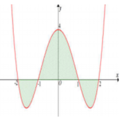
A. S = ∫ − 2 2 f x d x
B. S = 2 ∫ 0 2 f x d x
C. S = 2 ∫ 0 1 f x d x + 2 ∫ 1 2 f x d x
D. S = 2 ∫ 0 2 f x d x
D
Từ đồ thị của hàm số đối xứng qua trục tung nên đáp án A và B đúng.
Do ∫ 0 2 f x d x = ∫ 0 1 f x d x + − ∫ 1 2 f x d x
= ∫ 0 1 f x d x + − ∫ 1 2 f x d x
Nên đáp án C đúng. Vậy chọn đáp án D
Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y = f x trục hoành và hai đường thẳng x = a ; x = b a < b (phần tô đậm trong hình vẽ) tính theo công thức
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a b f x d x
C. S = ∫ a b f x d x
D. S = − ∫ a c f x d x + ∫ c b f x d x
Đáp án D.
Ta có
S = ∫ a c f x d x + ∫ c b f x d x = − ∫ a c f x d x + ∫ c b f x d x
Cho đồ thị ( C ) : y = ax 3 + bx 2 + cx + d và Parabol ( P ) : y = mx 2 + nx + p có đồ thị như hình vẽ (đồ thị (C) là đường cong đậm hơn). Biết phần hình phẳng được giới hạn bởi (C) và (P) (phần tô đậm) có diện tích bằng 1. Thể tích của khối tròn xoay tạo thành khi quay phần hình phẳng đó quanh trục hoành bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Đáp án D.

Ta có y ' = 4 a x 3 + 2 b x → y ' − 1 = − 4 a − 2 b . Phương trình tiếp tuyến của (C) tại điểm A − 1 ; 0 là đường thẳng
d : y = y ' − 1 . x + 1 ⇔ y = − 4 a − 2 b x − 4 a − 2 b
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C) là:
a x 4 + b x 2 + c = − 4 a + 2 b x − 4 a − 2 b ⇔ a x 4 + b x 2 + 4 a + 2 b x + 4 a + 2 b + c = 0 (*)
Quan sát đồ thị, ta thấy đường thẳng d cắt đồ thị tại hai điểm có hoành độ x = 0, x = 2 nên phương trình (*) có hai nghiệm x = 0, x = 2 .
Suy ra
4 a + 2 b + c = 0 16 a + 4 b + 2 4 a + 2 b + 4 a + 2 b + c = 0 ⇔ 4 a + 2 b + c = 0 28 a + 10 b + c = 0 (1)
Diện tích hình phẳng giới hạn bởi đường thẳng d, đồ thị (C) và hai đường thẳng x = 0, x = 2 là
S = ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 + b x 2 + c d x = 28 5
⇔ ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 − b x 2 − c d x = 28 5
⇔ − a 5 x 5 − b 3 x 3 − 2 a + b x 2 − 4 a + 2 b + c x 0 2 = 28 5
⇔ − 32 5 a − 8 b 3 − 4 2 a + b − 2 4 a + 2 b + c = − 28 5 ⇔ 112 5 a + 32 3 b + 2 c = 28 5 ( 2 )
Giải hệ phương trình gồm (1) và (2) ta tìm được: a = − 1, b = 3, c = − 2 .
Suy ra C : y = − x 4 + 3 x 2 − 2 và d : y = − 2 x − 2 . Diện tích hình phẳng cần tính là:
S = ∫ − 1 0 − x 4 + 3 x 2 − 2 − − 2 x − 2 d x = ∫ − 1 0 − x 4 + 3 x 2 + 2 x d x = ∫ − 1 0 x 4 − 3 x 2 − 2 x d x
= x 5 5 − x 3 − x 2 − 1 0 = 1 5 (đvdt).
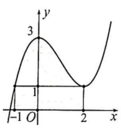
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f ( x ) = a x 3 + b x 2 + c , các đường thẳng x = - 1 , x = 2 và trục hoành (miền tô đậm) cho trong hình dưới đây
A. S = 51 8
B. S = 52 8
C. S = 50 8
D. S = 53 8
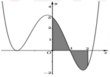
Cho hàm số y=f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x=0,x=2 (phần tô đen) là
A. S = - ∫ 0 1 f x d x + ∫ 1 2 f x d x
B. S = ∫ 0 1 f x d x - ∫ 1 2 f x d x
C. S = ∫ 0 2 f x d x
D. S = ∫ 0 2 f x d x
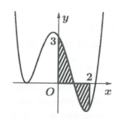
Cho hàm số y = f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C) trục hoành và hai đường thẳng x = 0 , x = 2 (phần tô đen) là
A. S = ∫ 0 1 f x d x - ∫ 1 2 f x d x
B. S = ∫ 0 2 f x d x
C. S = ∫ 0 1 f x d x + ∫ 1 2 f x d x
D. S = ∫ 0 2 f x d x