Thể tích của khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bới đồ thị hàm số y = x e x , trục hoành và đường thẳng x = 1 là:
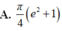
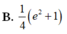
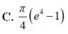
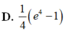
Thể tích của khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bới đồ thị hàm số y = x e x , trục hoành và đường thẳng x = 1 là
A. π 4 e 2 + 1
B. 1 4 e 2 + 1
C. π 4 e 4 - 1
D. 1 4 e 4 - 1
Thể tích của khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bới đồ thị hàm số y = x e x , trục hoành và đường thẳng x = 1 là:
A. π 4 e 2 + 1
B. 1 4 e 2 + 1
C. π 4 e 4 − 1
D. 1 4 e 4 − 1
Đáp án A
Xét pt tương giao: x e x = 0 ⇔ x = 0
⇒ V = π ∫ 0 1 x . e 2 x d x = π [ x e 2 x 2 − e 2 x 4 ] 1 0 = π 4 ( e 2 + 1 )
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y= x 4 - x 2 , trục Ox và đường thẳng x=1. Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox
A. V = π 2 ln 4 3
B. V = 1 2 ln 4 3
C. V = π 2 ln 3 4
D. V = π ln 4 3
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x 4 − x 2 , trục Ox và đường thẳng x = 1. Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox.
A. V = π 2 ln 4 3
B. V = 1 2 ln 4 3
C. V = π 2 ln 3 4
D. V = π ln 4 3
Đáp án A
Phương trình hoành độ giao điểm x 4 − x 2 = 0 ⇔ x = 0
Khi đó:
V = π ∫ 0 1 x 4 − x 2 d x = − π 2 ∫ 0 1 d 4 − x 2 4 − x 2 = − π 2 ln 4 − x 2 0 1 = π 2 ln 4 3
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 − x 2 , trục tung, đường thẳng x = 1 . Tính thể tích V của khối tròn xoay thu được khi quay hình H quanh trục Ox.
A. V = πln 2 4
B. V = πln 2 2
C. V = ln 2 4
D. V = ln 2 2
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 1 cos x ; y = 0; x = 0; x = π 3 Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là.
![]()
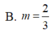
![]()
![]()
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 1 c o s x , y = 0 , x = 0 , x = π 3 . Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là
A. V = π
B. V = 2 π
C. V = π 3
D. V = π 2
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 1 ) e 2 x , trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
A. V = π 2 e 4 - 13
B. V = π 32 e 4 + 4
C. V = π 32 e 4 - 11
D. V = π 32 e 4 - 5
Tìm hoành độ giao điểm của hai dồ thị, ta có:
( x - 1 ) e 2 x = 0 => x = 1
Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi
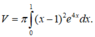
Đặt: u = ( x - 1 ) 2 , d v e 4 x d x . Ta có du = 2(x -1)dx và v = e 4 x 4 .
Áp dụng công thức tích phân từng phần ta được
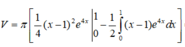
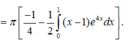
Đặt u 1 = x - 1 , d v 1 = e 4 x d x , ta có d u 1 = d x , v 1 = e 4 x 4
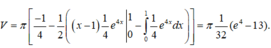
Vậy chọn đáp án A.
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =sinx.cosx, trục tung, trục hoành và đường thẳng x =π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V =π/16.
B. V = π 2 16
C. V = π 2 + π 16
D. V = π 2 4