Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , kí hiệu là z 1 và z 2 . Tính z 1 - z 2 2
A. 169.
B. 114244.
C. 338.
D. 676.
Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , kí hiệu là z 1 và z 2 .
Tính z 1 - z 2 2 .
A. 169
B. 114244
C. 338
D. 676
Cho biết có hai số phức z thỏa mãn z 2 = 119 − 120 i , kí hiệu là z 1 và z 2 . Tính z 1 − z 2 2 .
A. 169
B. 114244
C. 388
D. 676
Cho biết có hai số phức z thỏa mãn z 2 = 119 - 120 i , ký hiệu z 1 và z 2 . Tính | z 1 - z 2 | 2 .
A. 169.
B. 114244.
C. 338.
D. 676.
Gọi S là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 2 - 2 i ≤ 5 . Kí hiệu z 1 , z 2 là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính giá trị của biểu thức P = z 2 + 2 z 1 .
A. P = 2 6
B. P = 3 2
C. P = 33
D. P = 8
Gọi S là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 2 - 2 i ≤ 5 . Kí hiệu z 1 , z 2 là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính giá trị của biểu thức P = z 2 + 2 z 1 .
A. P= 2 6
B. P= 3 2
C. P= 33
D. P=8
Chọn C.
· ![]()
· Dấu “=” xảy ra khi:
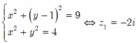
· 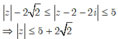
· Dấu “=” xảy ra khi:
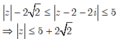
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính P = a 2 + b 2
A. P = 5
B. P = 7
C. P = 13
D. P = 25
Ta có
2
+
i
z
+
2
1
+
2
i
1
+
i
=
7
+
8
i
![]()
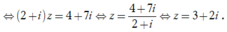
Suy ra 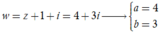
![]()
Chọn D.
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
![]()
![]()
![]()
![]()
Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
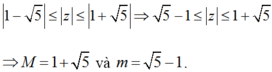
Vậy ![]()
Kí hiệu S là tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z − 1 + i = z + 2 i và điểm A là điểm biểu diễn số phức 1+2i. Biết rằng M ∈ S là điểm sao cho AM nhỏ nhất. Tung độ của điểm M là giá trị nào sau đây?
A. M − 1 ; 0
B. M 1 ; - 2
C. M − 1 ; 1
D. M 1 ; 1
Gọi S là tập hợp các số phức z thoả mãn z - i ≥ 3 và z - i ≤ 5 . Kí hiệu z 1 , z 2 là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính z 2 - z 1 .
A. z 2 - z 1 = 5 .
B. z 2 - z 1 = 2 10 .
C. z 2 - z 1 = 4 10 .
D. z 2 - z 1 = 10 .