Gọi S là tổng các giá trị nguyên của tham số m để phương trình 4 x + 7 = 2 x + 3 + m 2 + 6 m có nghiệm x ∈ 1 ; 3 . Chọn đáp án đúng.
A. S = -35
B. S = 20
C. S = 25
D. S = -31
Gọi S là tập hợp các giá trị nguyên của tham số m thuộc đoạn [−3;5] để phương trình x − m x + 1 = x − 2 x − 1 có nghiệm. Tổng các phần tử trong tập S bằng:
A. -1
B. 8
C. 9
D. 10
x − m x + 1 = x − 2 x − 1 ⇔ x ≠ ± 1 m x = m + 2
Phương trình đã cho có nghiệm ⇒ m ≠ 0 x = 1 + 2 m ≠ ± 1 ⇔ m ≠ 0 m ≠ 1
Vì m ∈ Z, m ∈ [−3; 5] nên m ∈ S = {−3; −2; 1; 2; 3; 4; 5}.
Đáp án cần chọn là: D
Gọi S là tập tất cả các giá trị nguyên của tham số m với m < 64 để phương trình log 1 5 x + m + log 5 2 - x = 0 có nghiệm. Tính tổng tất cả các phần tử của S
A. 2018
B. 2016
C. 2015
D. 2013
Gọi S là tập tất cả các giá trị nguyên của tham số m với m < 64 để phương trình log 1 5 x + m + log 5 2 - x = 0 có nghiệm. Tính tổng tất cả các phần tử của S .
A. 2018
B. 2016
C. 2015
D. 2013
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 − x + 1 − x = m + x − x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11
B. 0
C. 5
D. 6
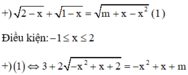
Đặt − x 2 + x = t ;
f x = − x 2 + x ; f ' x = − 2 x + 1
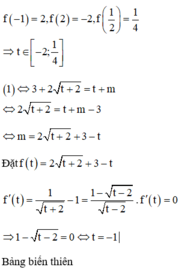
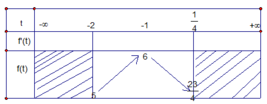

Chọn A
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.
Đáp án A
+)![]() (
(![]() )
)
Điều kiện:![]()
+)![]()
Đặt:![]()
![]()
![]()
![]()
![]()
Đặt![]()
![]() .
.![]()
Bảng biến thiên
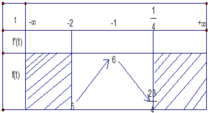
+) ![]()
Để phương trình có hai nghiệm phân biệt![]()
Do đó để phương trình có hai nghiệm phân biệt thì phương trình![]() có nghiệm
có nghiệm![]()
Từ bảng biến thiên![]() .
.
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m 2 x 4 - 16 + m x 2 - 4 - 28 x - 2 ≥ 0 đúng với mọi x ∈ R . Tổng giá trị của tất cả các phần tử thuộc S bằng
A. - 15 8
B. - 1
C. - 1 8
D. 7 8
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình cos 2 x − π 3 − m = 2 có nghiệm. Tính tổng T của các phần tử trong S.
A T= 6
B. T = - 6
C. T = 2
D. T = - 4
Phương trình cos 2 x − π 3 − m = 2 ⇔ cos 2 x − π 3 = m + 2.
Phương trình có nghiệm ⇔ − 1 ≤ m + 2 ≤ 1 ⇔ − 3 ≤ m ≤ − 1
→ m ∈ ℤ S = − 3 ; − 2 ; − 1 ⇒ T = − 3 + − 2 + − 1 = − 6.
Chọn đáp án B.
Gọi S là tập hợp các giá trị nguyên của tham số m để bất phương trình \(\dfrac{x^2-2x+4}{x^2-\left(3m+2\right)x+4}>0\) nghiệm đúng với mọi x. Tìm số phần tử của S.
A. 0 B. 5 C. 2 D. 3
( HEPL ME! )
Do \(x^2-2x+4=\left(x-1\right)^2+3>0;\forall x\) nên BPT đã cho nghiệm đúng với mọi x khi và chỉ khi:
\(x^2-\left(3m+2\right)x+4>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta=\left(3m+2\right)^2-16< 0\end{matrix}\right.\)
\(\Leftrightarrow9m^2+12m-12< 0\)
\(\Rightarrow-2< m< \dfrac{2}{3}\)
\(\Rightarrow m=\left\{-1;0\right\}\) có 2 giá trị
Cho phương trình (m+1)sinx + mcosx = 2m-1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm. Tính tổng tất cả các phần tử của S.
![]()
![]()
![]()
![]()