360⁰

Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.

Ta có:

$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$

$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$

$=540^0-180^0=360^0$

a. B = 55 độ

   C = 35

b. lỗi. phải là 360 độ

ông họ ngô

tôi họ đinh

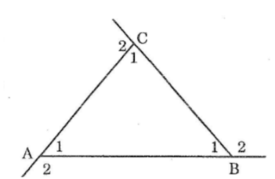
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)

∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)

∠(C1 ) +∠(C2 )=180o(hai góc kề bù)

Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o

⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)

Trong ΔABC, ta có:

∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o

Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.

180 độ là sai mk thử rùi

360 độ

Tick tớ́ nhé

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 180⁰
B^1 + B^2 = 180⁰
C^1 + C^2 = 180⁰
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180⁰
mà A^1 +B^1 +C^1 = 180⁰ (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180⁰ - 180⁰ = 2.180⁰ = 360⁰