Cho hai đường thẳng song song d 1 và d 2 . Trên đường thẳng d 1 có 10 điểm phân biệt, trên đường thẳng d 2 có 20 điểm phân biệt n ≥ 2 . Hỏi có tất cả bao nhiêu tam giác có đỉnh là các điểm đã cho.
A. 1000
B. 2000
C. 2400
D. 2800
Cho đường thẳng d: 3x-4y + 2=0. Có đường thẳng a và b cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là:
A. 3x+ 4y- 1= 0 ; 3x+ 4y + 5= 0
B. 3x-4y+7= 0 ; 3x-4y-3= 0
C. 3x+ 4y-3= 0 ; 3x+ 4y+ 7= 0
D.3x- 4y+ 6= 0; 3x-4y -4= 0
Giả sử đường thẳng ∆ song song với d : 3x- 4y+2= 0
Khi đó ; ∆ có phương trình là ∆ : 3x-4y +C= 0.
Lấy điểm M( -2 ; -1) thuộc d.

Do đó ; 2 đường thẳng thỏa mãn là:3x – 4y + 7 = 0 và 3x – 4y – 3 = 0
Chọn B
Số phát biểu đúng
1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy
3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
4. 2 đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
5. Nếu đường thẳng d không nằm trong mặt phẳng ( ) và d song song với đường thẳng d’ nằm trong ( ) thì d song song với ( )
6. Cho đường thẳng a song song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b song song với a
7. Nếu 2 mặt phẳng cùng song song với 1 đường thẳng thì giao tuyến của chúng ( nếu có ) cũng song song với đường thẳng đó
8. Cho 2 đường thẳng chéo nhau. Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
A. 8
B. 7
C. 6
D. 5
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
Trong các câu sau, câu nào đúng, câu nào sai?
a) Qua điểm A nằm ngoài đường thẳng d, chỉ có một đường thẳng song song với d.
b) Qua điểm A nằm ngoài đường thẳng d, có vô số đường thẳng song song với d.
c) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng a thì hai đường thẳng AB và AC trùng nhau.
d) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là x 1 = y + 1 2 = z 1 v à x 1 = y - 1 - 2 = z - 1 3 .Đường thẳng d cắt cả hai đường thẳng d₁, d₂ và song song với đường thẳng ∆ : x - 4 1 = y - 7 4 = z - 3 - 2 có phương trình là:
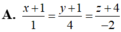
![]()
![]()
![]()
Chọn B
Gọi (P) là mặt phẳng chứa hai đường thẳng d₁ và d₂
Khi đó (P) đi qua M (0;-1;0) và có cặp véctơ chỉ phương ![]()
Gọi ![]() là VTPT của (P). Khi đó
là VTPT của (P). Khi đó ![]()
Phương trình (P): -8x+3y+2z+3=0
Gọi H là giao điểm của đường thẳng d₂ và (P):
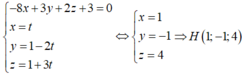
Đường thẳng d đi qua H và có VTCP ![]() có phương trình:
có phương trình:

Cho đường tròn (C): (x+ 1) 2 + (y-3)2 = 4 và đường thẳng d: 3x-4y + 5= 0. Phương trình của đường thẳng d’ song song với đường thẳng d và chắn trên (C) một dây cung có độ dài lớn nhất là:
A.3x – 4y + 1= 0
B. 3x - 4y +5 = 0
C.3x- 4y +15= 0
D.3x- 4y +10= 0
Đáp án C
Đường tròn (C) có tâm I( -1 ; 3) và bán kính R= 2
Do d’// d nên phương trình của d’ có dạng : 3x- 4y + c= 0.
Để d’ chắn trên (C) một dây cung có độ dài lớn nhất thì d’ phải đi qua tâm I của đường tròn ( trong các dây của đường tròn dây lớn nhất là đường kính).
Do I( -1 ; 3) thuộc d’ nên : 3.(-1) – 4.3 +c= 0
=> c = 15
Vậy đường thẳng cần tìm là d’ : 3x- 4y + 15= 0.
1) Cho hai đường thẳng y=2x-3(d) và y=3x-2(d')
a) Lập phương trình đường thẳng song song với (d) và cắt (d') tại điểm có hoành độ là 2
b)Lập phương trình đường thẳng vuông góc với (d') và cắt (d) tại điểm có tung độ là -1
1) Cho hai đường thẳng y=2x-3(d) và y=3x-2(d')
a) Lập phương trình đường thẳng song song với (d) và cắt (d') tại điểm có hoành độ là 2
b)Lập phương trình đường thẳng vuông góc với (d') và cắt (d) tại điểm có tung độ là -1
a) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_1\right)\).
Để \(\left(d_1\right)\)//\(\left(d\right)\) thì \(a=2\) \(\Rightarrow\left(d_1\right):y=2x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_1\right)\) và \(\left(d'\right)\):
\(2x+b=3x-2\Leftrightarrow x=b+2\).
Hai đường thẳng này cắt nhau tại điểm có hoành độ là 2
\(\Leftrightarrow b+2=2\Leftrightarrow b=0\).
Vậy phương trình đường thẳng cần lập là \(\left(d_1\right):y=2x\).
b) Gọi phương trình đường thẳng cần lập là \(y=ax+b\left(d_2\right)\).
\(\left(d_2\right)\perp\left(d'\right)\Leftrightarrow3a=-1\Leftrightarrow a=-\dfrac{1}{3}\)
\(\Rightarrow\left(d_2\right):y=-\dfrac{1}{3}x+b\).
Xét phương trình hoành độ giao điểm của \(\left(d_2\right)\) và \(\left(d\right)\):
\(2x-3=-\dfrac{1}{3}x+b\Leftrightarrow\dfrac{7}{3}x=b+3\Leftrightarrow x=\dfrac{3b+9}{7}\)
\(\Rightarrow y=2x-3=\dfrac{6b-3}{7}\).
Hai đường thẳng này cắt nhau tại điểm có tung độ bằng -1
\(\Leftrightarrow\dfrac{6b-3}{7}=-1\Leftrightarrow6b-3=-7\Leftrightarrow b=-\dfrac{2}{3}\).
Vậy phương trình đường thẳng cần lập là \(\left(d_2\right):y=-\dfrac{1}{3}x-\dfrac{2}{3}\).
Trên mặt phẳng tọa độ Oxy, cho đường thẳng \(d:2x+4y+1=0\) . Đường thẳng d' song song với đường thẳng d và tạo với tia Ox, Oy một tam giác có diện tích bằng 1. Tìm pt tổng quát của đường thẳng d'
Cho đường thẳng (d) y = -3x a) Vẽ đồ thị của hàn số trên b)Viết phương trình của đường thẳng(d') song song với đường thẳng (d) và có tung độ góc = 2 c)Vẽ đường thẳng(d') trên cùng mặt phẳng tọa độ d)Tìm tọa độ giao điểm của 2 đường thẳng (d) và (d')
c1:
Vì (d')//d nên pt đường thẳng của (d') là:y=-3x+b
đường thẳng (d') có tung độ gốc =2 => b=2
Vậy : pt đường thẳng của (d') là:y=-3x+2
Cho tam giác ABC có AM là đường trung tuyến ( M thuộc BC ) , D là điểm nằm giữa B và M . Qua D kẻ đường thẳng d song song với AM , đường thẳng d cắt hai đường thẳng AB , AC thứ tự tại E và F . Kẻ AK song song với BC ( K thuộc DF )
1. Chứng minh hai tam giác KAE và MBA đồng dạng với nhau
2. Chứng minh K là trung điểm của EF
3. Gọi N là trung điểm của AK , O là giao điểm của DN và AB . Xác định vị trí của điểm D trên đoạn thẳng BM để OD : ND = 2 : 5 ?