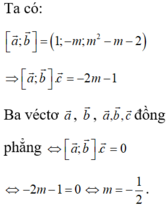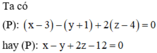Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto O M → theo ba vecto không đồng phẳng i → , j → , k → đã cho trên các trục Ox, Oy, Oz.

Những câu hỏi liên quan
Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto OM→ theo ba vecto không đồng phẳng i→,j→, k→ đã cho trên các trục Ox, Oy, Oz.
Trong không gian Oxyz, cho các vecto
a
→
(
m
;
1
;
0
)
,
b
→
(
2
;
m
-
1
;
1
)
,
c
→
(
1
;
m
+
1
;
1
)
. Tìm m để ba vecto
a
→
,
b
→
,
c...
Đọc tiếp
Trong không gian Oxyz, cho các vecto a → = ( m ; 1 ; 0 ) , b → = ( 2 ; m - 1 ; 1 ) , c → = ( 1 ; m + 1 ; 1 ) . Tìm m để ba vecto a → , b → , c → đồng phẳng
A. m= - 2
B. m = 3 2
C. m = - 1
D. m = - 1 2
Cho ba vecto
a
→
,
b
→
,
c
→
trong không gian. Chứng minh rằng nếu
m
a
→
+
n
b
→
+
p
c
→
0...
Đọc tiếp
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Giả sử p ≠ 0 ta có:
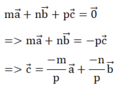
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
A
2
;
−
1
;
1
,
B
1
;
2
;
0
và
C
3
;
2
;
−
1...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 2 ; − 1 ; 1 , B 1 ; 2 ; 0 và C 3 ; 2 ; − 1 . Vecto nào dưới đây là một vecto pháp tuyến của mặt phẳng (ABC)?
A. n 1 → = 1 ; 1 ; 2
B. n 2 → = 1 ; - 1 ; 2
C. n 3 → = 1 ; 5 ; - 2
D. n 4 → = 2 ; 1 ; 1
Trong không gian Oxyz cho ba điểm A(2; -1; 3), B(4; 0; 1), C(-10; 5; 3). Hãy tìm tọa độ một vecto pháp tuyến của mặt phẳng (ABC).
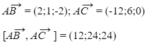
⇒ một vecto pháp tuyến của mặt phẳng (ABC) là n → (1;2;2)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho M(2;-1;1) và vecto
n
→
(
1
;
3
;
4
)
Viết phương trình mặt phẳng (P) đi qua điểm M và có vecto pháp tuyến
n
→
A. 2x - y + z + 3 0 B. 2x - y + z - 3 0 C. x + 3y + 4z + 3 0 D. x + 3y + 4z - 3 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho M(2;-1;1) và vecto n → = ( 1 ; 3 ; 4 ) Viết phương trình mặt phẳng (P) đi qua điểm M và có vecto pháp tuyến n →
A. 2x - y + z + 3 = 0
B. 2x - y + z - 3 = 0
C. x + 3y + 4z + 3 = 0
D. x + 3y + 4z - 3 = 0
Đáp án D
Phương trình mặt phẳng (P) đi qua điểm M và có vectơ pháp tuyến n → là:
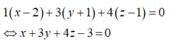
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho M(2;-1;1) và vecto
n
→
(
1
;
3
;
4
)
Viết phương trình mặt phẳng (P) đi qua điểm M và có vecto pháp tuyến
n
→
A. 2x - y + z +3 0 B. 2x - y + z -3 0 C. x + 3y + 4z +3 0 D. x + 3y + 4z - 3 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho M(2;-1;1) và vecto n → = ( 1 ; 3 ; 4 ) Viết phương trình mặt phẳng (P) đi qua điểm M và có vecto pháp tuyến n →
A. 2x - y + z +3 = 0
B. 2x - y + z -3 = 0
C. x + 3y + 4z +3 = 0
D. x + 3y + 4z - 3 = 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
1
;
1
;
0
,
B
0
;
−
1
;
2
.
Biết rằng có hai mặt phẳng cùng đi qua hai điểm O, A và cùng cách B một khoảng bằng
3
.
Vecto nào tron...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1 ; 1 ; 0 , B 0 ; − 1 ; 2 . Biết rằng có hai mặt phẳng cùng đi qua hai điểm O, A và cùng cách B một khoảng bằng 3 . Vecto nào trong các vecto dưới đây là một vecto pháp tuyến của một trong hai mặt phẳng đó?
A. n 1 → = 1 ; − 1 ; − 1 .
B. n 2 → = 1 ; − 1 ; − 3 .
C. n 3 → = 1 ; − 1 ; 5 .
D. n 4 → = 1 ; − 1 ; − 5 .
Đáp án D.
Phương pháp:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α . Viết phương trình mặt phẳng α .
Sử dụng các giả thiết O ∈ α ; A ∈ α ; d B ; α = 3 lập hệ phương trình tìm a, b, c.
Cách giải:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α .
O 0 ; 0 ; 0 ∈ α ⇒ α : a x + b y + c z = 0
A 1 ; 1 ; 0 ∈ α ⇒ a + b = 0 ⇒ b = − a ⇒ α : a x − a y + c z = 0
d B ; α = 3 ⇔ a .0 − a . − 1 + 2 c 2 a 2 + c 2 = 3 ⇔ a + 2 c 2 a 2 + c 2 = 3
⇔ a + 2 c 2 = 3 2 a 2 + c 2 ⇔ a 2 + 4 a c + 4 c 2 = 6 a 2 + 3 c 2 ⇔ 5 a 2 − 4 a c − c 2 = 0
Cho
a = 1 ⇒ c 2 + 4 c − 5 = 0 ⇔ c = 1 c = − 5 ⇒ n → 1 ; − 1 ; 1
hoặc n → 1 ; − 1 ; − 5 .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, mặt phẳng (P) đi qua điểm M(3;-1;4) đồng thời vuông góc với giá của vecto
a
→
1
;
-
1
;
2
có phương trình là A.
3
x
-
y
+
4
z
-
12
0
B.
3
x
-
y
+
4
z...
Đọc tiếp
Trong không gian Oxyz, mặt phẳng (P) đi qua điểm M(3;-1;4) đồng thời vuông góc với giá của vecto a → 1 ; - 1 ; 2 có phương trình là
A. 3 x - y + 4 z - 12 = 0
B. 3 x - y + 4 z + 12 = 0
C. x - y + 2 z - 12 = 0
D. x - y + 2 z + 12 = 0