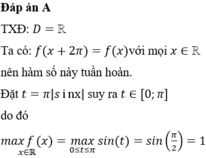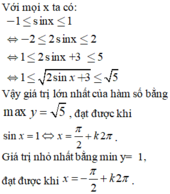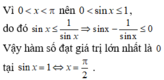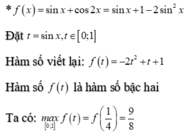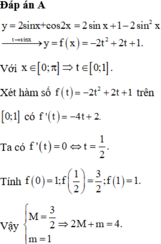Tìm giá trị lớn nhất của hàm số sau: y = 3 sin x - π 6 - 2

Những câu hỏi liên quan
Tìm giá trị lớn nhất và nhỏ nhất của hàm số : Y= 3/ 2+sin(π/3 +x)
\(sin\left(\dfrac{\pi}{3}+x\right)\in\left[-1;1\right]\)
\(\Rightarrow y=\dfrac{3}{2}+sin\left(\dfrac{\pi}{3}+x\right)\in\left[\dfrac{1}{2};\dfrac{5}{2}\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=\dfrac{1}{2}\\y_{max}=\dfrac{5}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
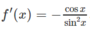
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số f ( x ) = sin ( π | sin x | ) .
A. 1
B. 1 4
C. 1 2
D. 0
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
sin
x
+
3
Đọc tiếp
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sin x + 3
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất của hàm số sau y = sinx - 1 sinx trong khoảng 0 < x < π
A: -1
B: 0
C: 1
D: 2
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y 2 sin x + cos 2x trên đoạn
0
,
π
. Khi đó 2M + m bằng A. 4 B. 5/2 C. 7/2 D. 5
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng
A. 4
B. 5/2
C. 7/2
D. 5
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 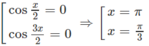
Ta có: f(0) = 0,
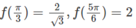
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Đúng 0
Bình luận (0)
Cho hàm số y=\(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\) với x thuộc \(\left(\dfrac{\text{π}}{4};\dfrac{\text{π}}{2}\right)\). Tìm giá trị nhỏ nhất của hàm số
y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ
Đúng 0
Bình luận (0)