Cho tam giác ABC vuông ở A và có BC=2AB=2a;a=17.56cm. Ở phía ngoài tam giác ABC vẽ hình vuông BCDEl, tam giác đều ABF và ACG. tính diện tích các tam giác AGF và BEF.

Những câu hỏi liên quan
Cho tam giác ABC vuông ở A có BC = 2AB = 2a. Ở phía ngoài tam giác vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG.
a. Tính các góc B, C ở cạnh BE và CG.
b. CMR: FA vuông góc với BE và CG. Tính diện tích tam giác FAG và tam giác FBE.
c. Tính diện tích tứ giác DEFG.
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
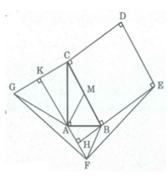
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính diện tích tứ giác DEFG
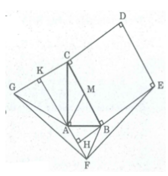
S B C D E = B C 2 = 2 a 2 = 4 a 2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: A H 2 + B H 2 = A B 2
⇒ B H 2 = A B 2 - A H 2 = a 2 - a 2 / 4 = 3 a 2 / 4 ⇒ BH = (a 3 )/2
S
A
B
F
= 1/2 BH.FA = 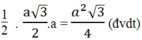
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: A C 2 = A K 2 + K C 2
⇒ A K 2 = A C 2 - K C 2 = 3 a 2 - 3 a 2 / 4 = 9 a 2 / 4 ⇒ AK = 3a/2 (đvdt)
S
A
C
G
= 1/2 AK.CG = 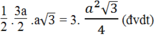
S D E F G = S B C D E + S F B E + S FAB + S F A G + S A C G + S A B C
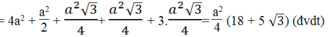
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.
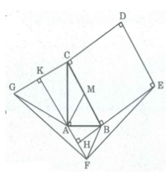
Ta có: ∠ (FAB) = ∠ (ABC) = 60 0
FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
BC ⊥ BE (vì BCDE là hình vuông)
Suy ra: FA ⊥ BE
BC ⊥ CD (vì BCDE là hình vuông)
Suy ra: FA ⊥ CD
Gọi giao điểm BE và FA là H, FA và CG là K.
⇒ BH ⊥ FA và FH = HA = a/2 (tính chất tam giác đều)
∠ (ACG) + ∠ (ACB) + ∠ (BCD) = 60 0 + 30 0 + 90 0 = 180 0
⇒ G, C, D thẳng hàng
⇒ AK ⊥ CG và GK = KC = 1/2 GC = 1/2 AC = (a 3 )/2
S
F
A
G
= 1/2 GK.AF = 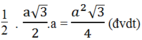
S F B E = 1/2 FH.BE = 1/2 .a/2 .2a = 1/2 a 2 (đvdt)
Đúng 0
Bình luận (0)
Cho Tam giác ABC vuông góc tại A , có BC =2AB=20cm ở phía ngoài Tam giác vẽ hình vuông BCDE, các tam giác đều ABF, ACG a, Tính góc B , góc C , cạnh AC , Diện tính ABC b, Chứng Minhh FA vg góc với BE và CG . tính Diện tính FAG và FBE
a: \(\widehat{C}=30^0\)
\(\widehat{B}=60^0\)
\(AC=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=5\cdot10\sqrt{3}=50\sqrt{3}\left(cm^2\right)\)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A có BC=2AB=2a. Gọi D là trung điểm của BC. Vẽ tam giác DEF vuông tại D có E thuộc AC, F thuộc AB.
a, Tính số đo các góc tam giác DEF
b, Tính diện tích tam giác DEF theo DE
c, Khi diện tích tam giác DEF nhỏ nhất, tính độ dài cung EF của đường tròn ngoại tiếp tam giác DEF
Cho tam giác ABC vuông tại A có BC=2AB=2a. Gọi D là trung điểm của BC. Vẽ tam giác DEF vuông tại D có E thuộc AC, F thuộc AB.
a, Tính số đo các góc tam giác DEF
b, Tính diện tích tam giác DEF theo DE
c, Khi diện tích tam giác DEF nhỏ nhất, tính độ dài cung EF của đường tròn ngoại tiếp tam giác DEF
cho tam giác abc vuông tại a có bc=2ab. tia phân giác góc b cắt ac tại .a, chứng minh bd=cd b, tính góc b và góc c của tam giác abc
a: Kẻ DK\(\perp\)BC
Xét ΔBAD vuông tại A và ΔBKD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)
Do đó: ΔBAD=ΔBKD
=>BA=BK
mà \(BA=\dfrac{1}{2}BC\)
nên \(BK=\dfrac{1}{2}CB\)
=>K là trung điểm của BC
Xét ΔDBC có
DK là đường cao
DK là đường trung tuyến
Do đó: ΔDBC cân tại D
b: ΔDBC cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)
=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)
=>\(\widehat{ABC}=90^0:\dfrac{3}{2}=90^0\cdot\dfrac{2}{3}=60^0\)
\(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}=\dfrac{1}{2}\cdot60^0=30^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có BC=2AB và \(\widehat{B}=2\widehat{C}\). CMR:tam giác ABC vuông tại A










