Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:
Những câu hỏi liên quan
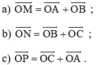
cho tam giác đều abc nội tiếp đường tròn tâm o, bán kính R. Từ một điểm M nằm trên cung nhỏ BC của đường tròn (O) kẻ MH, MI, MK lần lượt vuông góc với các đường thẳng AB, BC, CA. Xác định vị trí điểm M sao cho tổng d = MA + MB + MC + MH + MI + MK đạt gtln
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung
B
C
⏜
chứa A của (O). I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho
B
M
B
I
,
C
N
C
I
. Chứng m...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
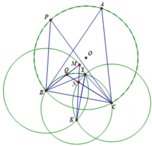
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.
Đúng 0
Bình luận (0)
cho△ABC có ba góc nhọn nội tiếp đường tròn tâm O , bán kính R. Hạ các đường cao AH,BK của tam giác . các tia AH,BK lần lượt cắt (O) tại các điểm thứ hai là D;E.
a)Chứng minh tứ giác AKHB nội tiếp một đường tròn. Xác định tâm của đường tròn đó
b)chứng minh rằng :HK song song với DE
a: góc AKB=góc AHB=90 độ
=>AKHB nội tiếp đường tròn đường kính AB
=>Tâm là trung điểm của AB
b: Gọi giao của AH và BK là M
ABHK là tứ giác nội tiếp
=>góc AHK=góc ABK
=>góc AHK=góc ADE
=>HK//DE
Đúng 0
Bình luận (0)
Cho đường tròn (O; R), tam giác ABC nội tiếp đường tròn. Gọi BM, CN lần lượt là các đường cao của tam giác ABC, I là trung điểm của BC.
a) Chứng minh bốn điểm B, N, M, C cùng thuộc một đường tròn. Xác định tâm của đường tròn đó.
b) Kẻ tia OI cắt đường tròn (O) tại E. Chứng minh tam giác BEC cân.
c) Giả sử R = 4 c m , B C = 4 3 c m , tính số đo góc BOC.
a:Xét tứ giác BNMC có
\(\widehat{BNC}=\widehat{BMC}=90^0\)
Do đó: BNMC là tứ giác nội tiếp
hay B,N,M,C cùng thuộc một đường tròn
Tâm là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi O là tâm đường tròn nội tiếp tam giác này. Trên BC lấy các
điểm M và N sao cho BM = BA; CN = CA. Chứng minh rằng O là tâm đường tròn ngoại tiếp tam
giác AMN.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BD,CE cắt nhau tại H. DE cắt BC tại F. Gọi K là giao điểm của AF với (O),N là giao điểm của KH
a) Chứng minh tứ giá BEDC nội tiếp. Xác định tâm M của đường tròn ngoại tiếp tứ giác BEDC
b ) Chứng minh góc FKE góc FDA
c ) Chứng minh AN là đường kính của đường tròn tâm O từ đó suy ra FH vuông góc với AM
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BD,CE cắt nhau tại H. DE cắt BC tại F. Gọi K là giao điểm của AF với (O),N là giao điểm của KH
a) Chứng minh tứ giá BEDC nội tiếp. Xác định tâm M của đường tròn ngoại tiếp tứ giác BEDC
b ) Chứng minh góc FKE= góc FDA
c ) Chứng minh AN là đường kính của đường tròn tâm O từ đó suy ra FH vuông góc với AM
Cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn tâm O, các đường cao BM,CN của tam giác cắt nhau tại H. Cho cạnh BC cô định, A thay đổi trên cung lớn BC sao cho tam giác ABC luôn nhọn. Xác định vị trí điể A để diện tích tam giác BCH lớn nhất
cho tam giác ABC đều nội tiếp đường tròn tâm O lấy M trên cung nhỏ BC trên dây AM lấy điểm D sao cho MD= MB
a) C/m tam giác MBD đều
b) C/m MB + MC = AM
c) C/m 4 điểm A, O, B, D thuộc 1 đường tròn
d) Xác định vị trí M trên cung BC nhỏ để MB+ MC lớn nhất.
Cho tam giác ABC đều. lấy các điểm M,N,P trên các cạnh AB,BC,CA sao cho AM = BN = CP
1) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh O là tâm đường tròn ngoại tiếp tam giác MNP
2) Gọi H,I,K lần lượt là trung điểm của AB,MP,AC. Chứng minh: H,I,K thẳng hàng
3) Xác định 3 cá điểm M,N,P để chu vi tam giác MNP nhỏ nhất
Giúp tớ với, mai tớ nộp rồi