Question

Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:

Answer 1

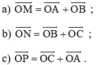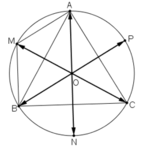
a) 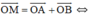 M là đỉnh còn lại của hình bình hành AOBM.

+ AOBM là hình bình hành ⇒ AM = OB

Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)

+ AOBM là hình bình hành ⇒ AM//BO

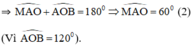
Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.

Mà 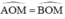 nên M là điểm chính giữa cung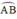 

b) Chứng minh tương tự phần a) ta có: 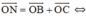 N là điểm chính giữa cung BC.

c) 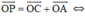 P là điểm chính giữa cung CA.