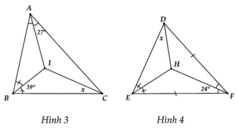
Tìm x trong mỗi hình vẽ sau biết I, H là giao điểm của ba đường phân giác của các góc trong của tam giác.
Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
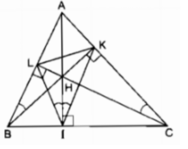
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có ![]()
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có ![]()
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có ![]()
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có ![]()
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có ![]()
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có 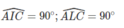
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai
Gọi I là giao điểm các phân giác trong tam giác ABC,O là giao điểm của ba đường trung trực của tam giác đó.Biết rằng BC là đường trung trực của OI.Tìm số đo các góc của tam giác ABC
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Trong Hình 8, I là giao điểm của ba đường phân giác của tam giác ABC.
a) Cho biết IM = 6 (Hình 8a). Tính IK và IN.
b) Cho biết IN = x + 3, IM = 2x – 3 (Hình 8b). Tìm x

a) Theo đề bài ta có AI, BI, CI là các phân giác của tam giác ABC
Mà I là giao điểm của 3 đường phân giác trong tam giác ABC
\( \Rightarrow \)IK = IN = IM = 6cm (Định lí về sự đồng quy của 3 đường phân giác trong tam giác)
b) Vì I là giao điểm của 3 đường phân giác trong tam giác ABC
\( \Rightarrow \) IK = IN = IM
\( \Rightarrow \) x + 3 = 2x – 3
\( \Rightarrow \) 3 + 3 = 2x – x
\( \Rightarrow \) x = 6
gọi i là giao điểm các phân giác trong tam giac abc, o là giao điểm của ba đường trung trực của tam giác đó . biết rằng bc là đường trung trực của oi . tìm số đo của tam giác abc
gọi i là giao điểm các phân giác trong tam giac abc, o là giao điểm của ba đường trung trực của tam giác đó . biết rằng bc là đường trung trực của oi . tìm số đo của tam giác abc
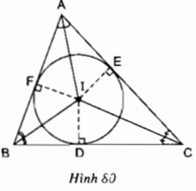
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
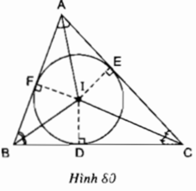
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
Cho tam giác ABC vuong tại a vẽ AH vuông góc BC tại H. Tia phân giác của góc HAB cắt BC ở D, tia phân giác của góc HAC cắt bc ở E. Chứng minh rằng giao điểm các đường phân giác của tam giác ABC là giao điểm các đường trung trực của tam giác ADE.(Dựa vào tính chất ba đường trung trực của tam giác