\(AC>AB\Rightarrow\widehat{B}>\widehat{C}\Rightarrow180^0-\widehat{B}< 180^0-\widehat{C}\Rightarrow\)Góc ngoài tại đỉnh B nhỏ hơn góc ngoài tại đỉnh C

a: Xét ΔABC có AB>AC

nên \(\widehat{B}< \widehat{C}\)

b: Vì \(\widehat{B}< \widehat{C}\)

nên góc ngoài tại đỉnh B lớn hơn góc ngoài tại đỉnhC

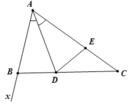
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:

∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)

∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)

Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)

Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)

Xét tam giác ABC có AC>AB

=>\(\widehat{ACB}\) >\(\widehat{ABC}\) (T/C góc và cạnh đối diện)

mà \(\widehat{ACB}\) + góc ngoài tại đỉnh C=180 độ

mà \(\widehat{ABC}\) + góc ngoài tại đỉnh B = 180 độ

=> Góc  ngoài tại đỉnh C>góc ngoài tại đỉnh B

Gọi E, F, P lần lượt là hình chiếu của I trên các đường thẳng AB, BC, CA.

Theo Định lí thuận ta có IE = IF và IF = IP => IE = IP .

Vậy I cách đều hai cạnh AB, AC.

Tham khảo

Gọi E, F, P lần lượt là hình chiếu của I trên các đường thẳng AB, BC, CA.

Theo Định lí thuận ta có IE = IF và IF = IP => IE = IP .

Vậy I cách đều hai cạnh AB, AC.