Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
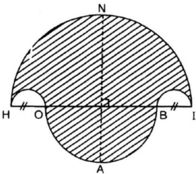
Hình 62
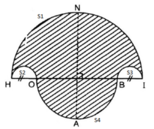
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
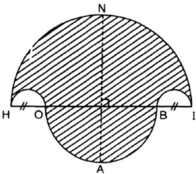
Hình 62
a) Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
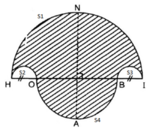
Diện tích miền gạch sọc bằng:
S = S 1 − S 2 − S 3 + S 4
với:
+ S 1 là nửa đường tròn đường kính HI
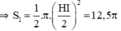
+ S 2 ; S 3 là nửa đường tròn đường kính HO và BI.
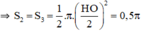
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
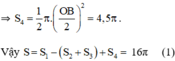
c)Ta có: 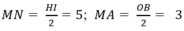
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π 4 2 = 16 π ( c m 2 ) ( 2 )
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
Tính diện tích hình HOABINH (miền gạch sọc).
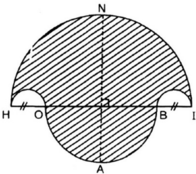
Hình 62
Diện tích miền gạch sọc bằng:
S = S1 – S2 – S3 + S4
với:
+ S1 là nửa đường tròn đường kính HI
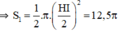
+ S2; S3 là nửa đường tròn đường kính HO và BI.
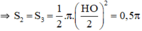
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
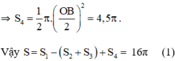
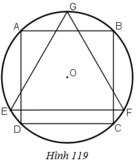
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
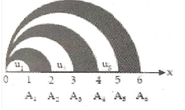
Trên tia Ox lấy các điểm A 1 , A 2 , . . . , A n , . . . sao cho với mỗi số nguyên dương n, O A n = n . Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính O A n , n=1,2... Kí hiệu u 1 là diện tích của nửa hình tròn đường kính O A 1 và với mỗi n ≥ 2 , kí hiệu u n là diện tích của hình giới hạn bởi nửa đường tròn đường kính O A n - 1 , nửa đường tròn đường kính O A n và tia Ox. Chứng minh rằng dãy số ( u n ) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
A. d = π 4
B. d = π 2
C. d = π 3
D. d = 2 π 3
a/ Viết công thức tính diện tích hình tròn ( Viết kí hiệu) b/ Một hình tròn có bán kính 6 cm. Tính diện tích hình tròn đó b/ Một hình tròn có đường kính 10 dm. Tính diện tích hình tròn đó
a)S=2x\(\pi\)xR
b)S=2x3,14x6=37,68
c)S=10x3,14=31,4
Hai nửa hình tròn có cùng đường kính nên tổng diện tích hai nửa hình tròn này bằng đúng diện tích của một hình tròn có đường kính bằng 6 cm
-Nếu bán kính của hình tròn giảm đi 10% thì diện tích của hình tròn đó giảm đi bn % ?
-Nếu bán kính của hình tròn giảm đi 20% thì diện tích của hình tròn đó giảm đi bn % ?
-Nếu đường kính của hình tròn giảm đi 20% thì diện tích của hình tròn đó giảm đi bn % ?
-Nếu đường kính của hình tròn giảm đi 50% thì diện tích của hình tròn đó giảm đi bn % ?
-Nếu đường kính của hình tròn giảm đi 60% thì diện tích của hình tròn đó giảm đi bn %?
- Giảm 19% (90%x r x 90% x r = 81% x S => S - 81% x S = 19% x S )
- Giảm 36%
- Giảm 19%
- Giảm 43,75%
- Giảm 51%
Coi cạnh hình vuông ban đầu là 100% thì cạnh hình vuông lúc sau chiếm là :
100% - 10% = 90% (cạnh ban đầu)
Diện tích hình vuông lúc đầu là :
100% x 100% = 100%
Diện tích hình vuông lúc sau là :
90% x 90% = 81%
Sau khi giảm cạnh hình vuông thì diện tích hình vuông sẽ giảm đi số phần trăm là:
100% - 81% = 9 %
Đáp số : 9%
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
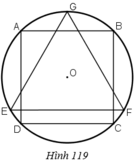
Hình 119
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO'
a) Chứng minh rằng mặt cầu đường kính OO' tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ
b) Cắt hình trụ bởi một mặt phẳng song song với trục OO' và cách trục một khoảng bằng \(\dfrac{r}{2}\). Tính diện tích thiết diện thu được
c) Thiết diện nói trên cắt mặt cầu đường kính OO' theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó