Ta có: 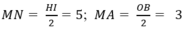
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π42 = 16π (cm2) (2)
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
Ta có: 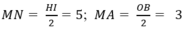
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π42 = 16π (cm2) (2)
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
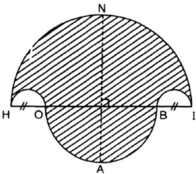
Hình 62
Tính diện tích hình HOABINH (miền gạch sọc).
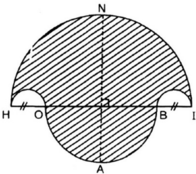
Hình 62
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
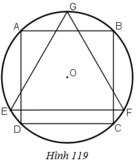
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
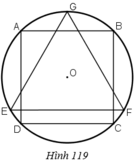
Hình 119
B2: Cho hình nón như hình bên: Biết rằng đáy là hình tròn có bán kính bằng 3cm, đường sinh có độ dài là 5cm. Hãy tính:
1) Diện tích xung quanh, diện tích toàn phần
2) Thể tích của hình nón đó.
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
cho đường tròn đường kính 38cm. Tính diện tích hình tròn. Tính chiều dài (a) và chiều rộng (b) của hình chữ nhật có cùng diện tích với hình tròn đó biết ti lệ: \(\frac{a}{b}=\frac{1+\sqrt{5}}{2}\) (tỉ lệ vàng). (làm tròn đến chữ số thập phân thứ nhất)
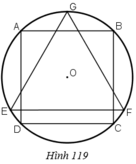
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
cho hình bình hành ABCD , có đỉnh D nằm trên đường tròn , đường kính bằng 2R . hạ BN và DM cùng vuông góc với đường chéo AC
a) Chứng minh C,B,M,D cùng thuộc 1 đường tròn
b) Chứng minh DB.DC=DN.AC
c) Xác định vị trí điểm D để hình bình hành ABCD có diện tích lớn nhất và tính diện tích của hình bình hành trong trường hợp này
mọi người giải giúp dùm nhá