Ta có: \(\widehat B = {65^o},\widehat C = {85^o}.\)

\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.\)

Áp dụng định lí sin trong tam giác ABC, ta có:

\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\)

Mà \(\widehat A = {30^o},R = 6.\)

\( \Rightarrow BC = 2.6.\sin {30^o} = 6.\)

Vậy BC = 6.

a)

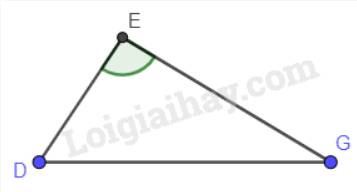
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.

Vậy DE < DG.

b)

Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ  - 56^\circ  - 65^\circ  = 59^\circ \).

Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).

a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)

Có: ^OBC = ^OBA ( BF là phân giác ^B)

mà:  ^EOB = ^OBC (cmt)

=> ^EOB = ^OBA => tam giác EBO cân tại E

Có: ^OCA = ^OCB ( BF là phân giác ^B)

mà:  ^FOC = ^OCB (cmt)

=> ^FOC = ^OCA => tam giác FCO cân tại E

Ta có: ^AEF = ^B (cmt)

           ^AFE = ^C (cmt)

Mà ^B = ^C (tam giác ABC cân tại A)

=> ^AEF =  ^AFE => tam giác AEF cân tại A

Có : ^ABF = ^CBF =  \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)

       ^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)

mà : ^B = ^C (tam giác ABC cân tại A)

=> ^ACE = ^ABF = ^CBF = ^BCE

Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O

Xét tam giác FCO và tam giác EBO có:

^FOC = ^FOB ( đối đỉnh)

^FCO = ^EBO (^ABF = ^ACE)

OB = OC ( tg OBC cân tại O )

=> tam giác FCO = tam giác EBO(g-c-g)

Ta có A = 180o - 70o - 45o = 65o.

Vì góc C là góc nhỏ nhất nên cạnh AB nhỏ nhất. Chọn A

Vì AC là cạnh nhỏ nhất nên góc B là góc nhỏ nhất. Chọn B

Do BC là cạnh nhỏ nhất nên góc C là góc nhỏ nhất. Chọn C

Bài2 , 

Ta có\(sin_P^2+cos_P^2=1\)

mà \(2\left(sin_P^2+cos_P^2\right)\ge\left(sin_P+cos_p\right)^2\Rightarrow\left(sin_p+cos_p\right)\le\sqrt{2}\)

^_^