Trong các hàm số sau, hàm số nào nghịch biến trên ℝ ?
A. y = log 3 x 2
B. y = log ( x 3 )
C. y = e 4 x
D. y = 2 5 - x
Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?
a) \(y = {\left( {\frac{{\sqrt 3 }}{2}} \right)^x}\)
b) \(y = {\left( {\frac{{\sqrt[3]{{26}}}}{3}} \right)^x}\)
c) \(y = {\log _\pi }x\)
d) \(y = {\log _{\frac{{\sqrt {15} }}{4}}}x\)
\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số y = f x có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f ' x như hình bên dưới

Hàm số g x = f 1 - x + x 2 2 - x nghịch biến trên khoảng nào trong các khoảng sau?
A. (-3;1)
B. (-2;0)
C. - 1 ; 3 2
D. (1;3)
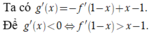
Đặt t = 1 - x, bất phương trình trở thành f'(t) > -t
Kẻ đường thẳng y = -x cắt đồ thị hàm số f'(x) lần lượt tại ba điểm x = -3, x = -1, x = 3 (như hình vẽ)
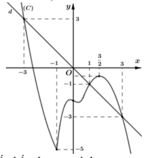
Quan sát đồ thị ta thấy bất phương trình
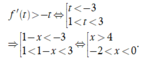
Đối chiếu đáp án ta chọn B.
Trong các hàm số sau, hàm số nào nghịch biến trên ℝ ?
A. y = log 3 x 2 .
B. y = log x 3 .
C. y = e 4 x .
D. y = 2 5 − x .
Trong các hàm số sau, hàm số nào nghịch biến trên ℝ?
A. y = log 3 x 2
B. y = log x 3
C. y = e 4 x
D. y = 2 5 - x
Hàm số nào trong các hàm số sau đây nghịch biến trên tập ℝ
A. y = - x 3 + x 2 - 10 x + 1
B. y = x 4 + 2 x 2 - 5
C. y = x + 1 x 2 + 1
D. y = cot 2x
Hàm số nào trong các hàm số sau đây nghịch biến trên tập ℝ
A. y = - x 3 + x 2 - 10 x + 1
B. y = x 4 + 2 x 2 - 5
C. y = x + 1 x 2 + 1
D. y = cot2x
Chọn A.
Ta loại ngay hai đáp án D (có TXĐ không phải ℝ ) và B ( luôn có cả khoảng đồng biến và nghịch biến).
Kiểm tra đáp án A ta có:
![]()
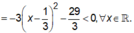
do đó hàm số nghịch biến trên ℝ suy ra chọn đáp án A.
Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực ℝ ?
A. y = 2 e x
B. y = π 3 x
C. y = log π 4 2 x 2 + 1
D. y = log 1 2 x
Cho hàm số f(x) có đạo hàm liên tục trên ℝ . Bảng biến thiên của hàm số f’(x) trên đoạn [-1;3] như hình
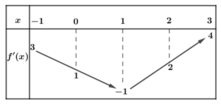
Hàm số g x = f 1 - x 2 + x nghịch biến trên khoảng nào trong các khoảng sau ?
A. (-4;-2)
B. (-2;0)
C. (0;2)
D. (2;4)
Ta có ![]()
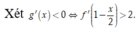
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 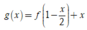 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.