Cho các số sau 2;8;1;0;1;9;9;5 được viết trên một vòng tròn theo thứ tự ngẫu nhiên. Mỗi lần, ta chọn hai số cạnh nhau bất kì và cộng thêm mỗi số 1 đơn vị. Hỏi sau một số lần thực hiện thao tác trên các số trong vòng tròn có có thể đều bằng nhau không?
HELP MIK
Cho 12 số tự nhiên từ số 1 đến số 12. Có thể sắp xếp 12 số này trên một vòng tròn sao cho 2 số kề nhau bất kỳ có tổng lớn hơn 12 hay không? Vì sao?
không thể vì sẽ có số 1 với số bất kì 1<n<12
Vậy 2<1 + n<13
K thể xếp đc 12 số này trên một vòng tròn sao cho 2 số kề nhau bất kỳ có tổng lớn hơn 12
Bởi dù xếp thế nào cũng sẽ có 1 số có 1+n(1 số bất kì)<12
Cho tập hợp{1;2;3;...;2016}Tìm số số nguyên lớn nhấtcó thể chọn từ tập hợp trên sao cho các số được chọn khác nhau khi sắp xếp các số trên một vòng tròn thì tích của hai số bất kiflieenf kề nhau không vượt quá 100.
Tìm ba số tự nhiên khác nhau và khác không vào ba hình tròn ở các đỉnh sao cho tổng hai hình tròn trên một cạnh luôn được kết quả là một số chính phương ?
Không lo đâu, làm như theo tôi là được. Như thế này:
Chúc học tốt! -_-
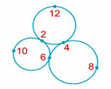
Điền số trên đường tròn Điền 6 số chẵn từ 2 đến 12 vào các chấm trên 3 vòng tròn sao cho tổng 3 số nằm trên mỗi vòng tròn đều bằng 18.
Sáu số chẵn đó là: 2, 4, 6, 8, 10, 12.
Ta có: 18 = 2 + 4 + 12
18 = 2 + 6 + 10
18 = 4 + 6 + 8
Trên hình vẽ ta thấy cứ hai đường tròn lại có một điểm chung. Như vậy số nào điền vào điểm chung đó sẽ thuộc hai tổng đã cho. Ta thấy số 2, số 4, số 6 đều lặp lại hai lần nên ba số đó được điền vào ba điểm chung. Các số đã cho được điền vào hình vẽ như sau:
Cho các số 2; 8; 1;0; 1; 9; 9; 5 được viết trên một vòng tròn theo thứ tự ngẫu nhiên. Mỗi lần
ta chọn hai số cạnh nhau bất kì và cộng thêm mỗi số 1 đơn vị. Hỏi sau một số lần thực hiện thao
tác trên các số trên vòng tròn đó có có thể đều bằng nhau không?
Làm một vòng tròn nhỏ bằng bìa cứng, trên dán giấy trắng. Chia vòng tròn thành 3 phần đều nhau: một phần tô màu đỏ, một phần tô màu lục và một phần tô màu lam. Làm thêm một trục quay đi qua tâm của vòng tròn sao cho vòng tròn quay được như một con quay. Cho vòng tròn quay tít dưới ánh sáng ban ngày. Nhận xét về màu của giấy lúc đó. Có thể coi đây là một thí nghiệm trộn các ánh sáng màu với nhau được không?
Thí nghiệm này gọi là thí nghiệm đĩa tròn Niu-tơn. Do hiện tượng lưu ảnh trên màng lưới, nên nếu đĩa quay nhanh, mỗi điểm trên màn lưới nhận được gần như đồng thời ba thứ ánh sáng phản xạ từ ba vùng các màu đỏ, lục, lam trên đĩa chiếu đến và cho ta cảm giác màu trắng. Không thể coi đây là một thí nghiệm trộn ánh sáng màu với nhau được.
Thí nghiệm này được gọi là thí nghiệm đĩa tròn Niu-tơn. Do hiện tượng lưu ảnh trên màng lưới của mắt ta, nên nếu đĩa quay nhanh, mỗi điểm trên màng lưới nhận được gần như là đồng thời ba thứ ánh sáng phản xạ từ ba vùng có các màu đỏ, lục làm trên đĩa chiếu đến và cho ta cảm giác màu trắng. Cũng có thể coi đây là một thí nghiệm trộn các ánh sáng màu với nhau.
Cho tập hơp 1;2;3;...;2016 Tìm số nguyên lơns nhất có thể chọntuwf tập hợp trên sao cho các số đc chọn khác nhau khi sắp xếp các số trên một vòng tròn thì tích của hai số bất kì liền kề nhau không vượt quá 100
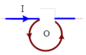
Một dây dẫn rất dài được căng thẳng trừ một đoạn ở giữa dây uốn thành một vòng tròn bán kính 1,5cm. Cho dòng điện 3A chạy trong dây dẫn. Xác định cảm ứng tù tại tâm của vòng tròn nếu vòng tròn và phần dây thẳng cùng nằm trong một mặt phẳng, chỗ bắt chéo hai đoạn dây không nối với nhau.
A. 5 , 6.10 − 5 T .
B. 16 , 6.10 − 5 T .
C. 17 , 6.10 − 5 T .
D. 18 , 6.10 − 5 T .
Có 17 viên bi, trong đó 6 viên R, 6 viên B và 5 viên Y được đánh số từ 1 đến 17 và bố trí trên vòng tròn như trong hình vẽ. Với số điểm ban đầu là 0, ở mỗi bước em hãy lấy ra khỏi vòng tròn tất cả các viên bi cùng loại kề nhau có số lượng lớn hơn 1. Nếu số bi lấy ra được là k thì sau bước này số điểm tăng thêm k×k (k nhân k) điểm. Các viên bi còn lại sẽ dồn sát với nhau thành một vòng tròn nhỏ hơn. Em hãy tìm một cách lấy bi theo quy tắc nêu trên để lấy hết bi ra khỏi vòng tròn và tổng số điểm nhận là lớn nhất có thể.
