Cho 2 vec tơ a → ( a 1 ; a 2 ) ; v à b → ( b 1 ; b 2 ) . Biểu thức sai là:
A. ![]()
B.![]()
C. 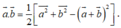
D.![]()
giúp mik ba bài này với ^-^
1. Cho hình chữ nhật ABCD có AB = 3a , AD = 4a
a) Tính / vec tơ AD - vec tơ AB / b) Dựng vec tơ u = vec tơ CA - vec tơ AB . Tính / vec tơ u /
2. Cho △ABC đều cạnh a . Gọi I là trung điểm BC
a) Tính / vec tơ AB - vec tơ AC / b) Tính / vec tơ BA - vec tơ BI /
3. Cho △ABC vuông tại A . Biết AB = 6a , AC = 8a . Tính / vec tơ AB - vec tơ AC /
mn ơi giúp mik với ,ai biết làm thì làm hết hộ mik nha còn ko làm hết được làm hộ mik 1 trong mấy
câu đó th T-T
1 Cho 8 điểm A , B, C, D , E , F , G ,H . CMR
vec tơ AC + vec to BF + vec tơ GD + vec tơ HE = vec tơ AD + vec tơ BE + vec tơ GC + vec tơ HF
2 Cho tam giác ABC , từ A , B , C dựng 3 vec tơ tùy ý vec tơ AA' , vec tơ BB' , vec tơ CC'
CMR : vec tơ AA' + vec tơ BB' + vec tơ CC' = vec tơ BA' + vec tơ CB' + vec tơ AC'
3 Gọi O là tâm của hbh ABCD , CMR :
a) vec tơ DO + vec tơ AO = vec tơ AB
b) vec tơ OD + vec tơ OC = vec tơ BC
c ) vec tơ OA + vec tơ OB + vec tơ OC + vec tơ OD = vec tơ 0
d) vec tơ MA + vec tơ MC = vec tơ MB + vec tơ MD ( với M là 1 điểm tùy ý )
help me
mn ơi giúp mik bài này với , mik đang cần gấp
cho tam giác ABC
a. tìm điểm I sao cho 2 vec tơ IB 2 vec tơ IB + 3 vec tơ IC = vec tơ 0
b. tìm điểm J sao cho vec tơ JA - vec tơ JB - 2 vec tơ JC = vec tơ 0
c. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC = vec tơ BC
d. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC = 2 vec tơ BC
e. tìm điểm L sao cho 3 vec tơ LA - vec tơ LB + 2 vec tơ LC = vec tơ 0
giải hộ mik bài này với
Cho △ABC . Hãy xác định điểm M sao cho :
a) vec tơ MA - vec tơ MB + vec tơ MC = vec tơ 0 b) vec tơ MB - vec tơ MC + vec tơ BC = vec tơ 0
c) vec tơ MB - vec tơ MC + vec tơ MA = vec tơ 0 d) vec tơ MA - vec tơ MB - vec tơ MC = vec tơ 0
e) vec tơ MC + vec tơ MA - vec tơ MB + vec tơ BC = vec tơ 0
Cho hbh ABCD tâm O. M là điểm bất kì nằm trong mặt phẳng. CM: a) vec tơ OA + vec tơ OB + vec tơ OC + vec tơ OD= vec tơ O b) vec tơ MA + vec tơ MC = vec tơ MB + vec tơ MD
Lời giải:
Vì $O$ là tâm hình bình hành nên $O$ là trung điểm của $AC, BD$
$\Rightarrow \overrightarrow{OA}, \overrightarrow{OC}; \overrightarrow{OB}, \overrightarrow{OD}$ là 2 cặp vecto đối nhau
$\Rightarrow \overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$
$\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$ (đpcm)
b) Theo phần a ta có:
\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC}\)
\(=\overrightarrow{MO}+\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{MO}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{OD}\)
\(=(\overrightarrow{MO}+\overrightarrow{OB})+(\overrightarrow{MO}+\overrightarrow{OD})=\overrightarrow{MB}+\overrightarrow{MD}\) (đpcm)
mn giúp mik với ạ , lần đầu tham gia nhóm
cho 4 điểm A, B, C, D
a) CMR vec tơ AB + vec tơ CD = vec tơ AD + vec tơ BD
b) CM nếu vec tơ AB = vec tơ CD thì vec tơ AC = vec tơ BD
c) Với điều kiện nào thì vec tơ AB + vec tơ AC là đường phân giác trong của góc BAC
câu a phải là CM \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\) chứ nhỉ?
a/ \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)
\(=\overrightarrow{AD}+\overrightarrow{CB}\)
b/ \(\overrightarrow{AB}=\overrightarrow{CD}\Leftrightarrow\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{CB}+\overrightarrow{BD}\)
\(\Leftrightarrow\overrightarrow{AC}=\overrightarrow{BD}\)
Câu c nghe nó sai sai kiểu j ấy, \(\overrightarrow{AB},\overrightarrow{AC}\) tạo thành \(\widehat{BAC}\) rồi thì làm sao thành phân giác đc :))
cho tứ giac ABCD .Goij M và N lần lượt là trung điểm của AB và CD. lấy các điểm P ,Q lần lươt thuộc các đường thẳng AD và BC sao cho vec tơ PA=-2 vec tơ PD, vec tơ QP =-2 vec tơ QC. tính vec tơ MN?? giúp tui
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?
a) a→ (-3; 0) và i→ (1; 0) là hai vec tơ ngược hướng.
b) a→ (3; 4) và b→ (-3; -4) là hai vec tơ đối nhau
c) a→ (5; 3) và b→ (3; 5) là hai vec tơ đối nhau.
d) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
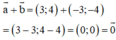
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
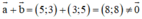
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Cho hai vec tơ a→ và b→ có a → = 3 , b → = 3 , a → , b → = 120 ° . Với giá trị nào của m thì hai vec tơ a → + m b → v à a → - m b → vuông góc với nhau?