Cho tứ giác ABCD. Điều kiện cần và đủ để A B → = C D → ?
A. ABCD là hình bình hành
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm
D. AB= CD
Những câu hỏi liên quan
Phần I:Trắc nghiệmTrong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để tứ giác ABCD là hình bình hành? A.
O
A
→
+
O
B
→
+
O
C
→
+
O
D
→
0...
Đọc tiếp
Phần I:Trắc nghiệm
Trong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để tứ giác ABCD là hình bình hành?
A. O A → + O B → + O C → + O D → = 0 →
B. O A → + O C → = O B → + O D →
C. O A → + 1 2 O B → = O C → + 1 2 O D →
D. O A → + 1 2 O C → = O B → + 1 2 O D →
Chọn B.
- Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
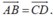
- Với mọi điểm O bất kì khác A, B, C, D ta có:
Đúng 0
Bình luận (0)
1.Trong các mệnh đề sau, mệnh đề nào sai ?A. để tứ giác ABCD là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau.B. Để x^2 25 điều kiện đủ là x 2 .C. Để tổng a + b của hai số nguyên a, b chia hết cho 13, điều kiện đủ là mỗi số đó chia hết cho 13.D. Để có ít nhât một trong hai số a, b là số dương điều kiện đủ là a + b 0 .2.Trong các mệnh đề sau, mệnh đề nào đúng ?A. Để tứ giác T là một hình vuông, điều kiện cần và đủ là nó có bốn cạnh bằng nhau.B. Để tổng hai số tự nh...
Đọc tiếp
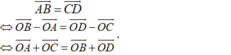
1.Trong các mệnh đề sau, mệnh đề nào sai ?
A. để tứ giác ABCD là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau.
B. Để x^2 = 25 điều kiện đủ là x = 2 .
C. Để tổng a + b của hai số nguyên a, b chia hết cho 13, điều kiện đủ là mỗi số đó chia hết cho 13.
D. Để có ít nhât một trong hai số a, b là số dương điều kiện đủ là a + b > 0 .
2.Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Để tứ giác T là một hình vuông, điều kiện cần và đủ là nó có bốn cạnh bằng nhau.
B. Để tổng hai số tự nhiên chia hết cho 7, là mỗi số đó chia hết cho 7.
C. Để ab > 0, điều kiện cần là cả hai số a và b đều dương.
D. Để một số nguyên dương chia hết cho 3, điều kiện cần là nó chia hết cho 9.
Trong không gian cho điểm O bất kì và bốn điểm A, B, C, D không thẳng hàng. Chứng minh điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: O A → + O C → = O B → + O D →
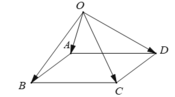
+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: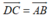 
.
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
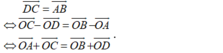
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Điều kiện cần và đủ để
A
B
→
C
D
→
? A. ABCD là hình bình hành B. ABDC là hình bình hành. C. AD và BC có cùng trung điểm D. AB CD
Đọc tiếp
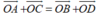
Cho tứ giác ABCD. Điều kiện cần và đủ để A B → = C D → ?
A. ABCD là hình bình hành
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm
D. AB= CD
Cho tứ giác ABCD. Phát biểu một điều kiện cần và đủ để :
a) ABCD là một hình bình hành
b) ABCD là một hình chữ nhật
c) ABCD là một hình thoi
a) Tứ giác ABCD là một hình bình hành khi và chỉ khi AB // CD và AB = CD
b) Tứ giác ABCD là một hình chữ nhật khi và chỉ khi nó là một hình bình hành và có một góc vuông
c) Tứ giác ABCD là một hình thoi khi và chỉ khi nó là một hình bình hành và có hai đường chéo vuông góc với nhau
Đúng 1
Bình luận (0)
Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA của tứ giác ABCD.
a, C/minh: Tứ giác MNPQ là hình bình hành
b, Tứ giác MNPQ là hình chữ nhật thì tứ giác ABCD cần thêm điều kiện gì?
c, Tứ giác MNPQ là hình thoi thì tứ giác ABCD cần thêm điều kiện gì?
d, Để tứ giác MNPQ là hình vuông thì tứ giác ABCD cần thêm điều kiện gì?
Câu 4:Trong các mệnh đề sau, mệnh đề nào sai? A. Để tứ giác là hình bình hành, điều kiện cần và đủ là hai cạnh đối song song và bằng nhau. B. Để điều kiện đủ là . C. Để tổng của hai số nguyên chia hết cho 13, điều kiện cần và đủ là mỗi số đó chia hết cho 13. D. Để có ít nhất một trong hai số là số dương điều kiện đủ là .
Cho hình bình hành ABCD. Gọi E. F lần lượt là trung điểm của AB và CD, G và H lần lượt là giao điểm của BD với AF và CE.
a, C/minh: Tứ giác AECF, GEHF là hình bình hành
b, C/minh: DG = GH = HB
c, Để tứ giác GEHF là hình chữ nhật thì hình bình hành ABCD cần thêm điều kiện gì ?
d, Để tứ giác GEHF là hình thoi thì hình bình hành ABCD cần thêm điều kiện gì ?
cho tứ giác ABCD gọi E<F<G<H là trung điểm các cạnh AB<BC<CD<DA luần lượt:
a, Chứng minh tứ gaics AFGH là hình bình hành.
b, tìm điều kiện của tứ giác ABCD để EFGH là hình thoi.
c, tìm điều kiện của tứ giác ABCD để EFGH là hình chữ nhật.
d, tìm điều kiện của tứ giác ABCD để EFGH là hình vuông
E, F lần lượt là trung điểm của AB và BC (gt)
\(\Rightarrow\) EF là đường trung bình của tam giác ABC
\(\Rightarrow\) EF // AC và EF = \(\frac{1}{2}\) AC (1)
H, G lần lượt là trung điểm của AD và DC (gt)
\(\Rightarrow\) HG là đường trung bình của tam giác ACD
\(\Rightarrow\) HG // AC và HG = \(\frac{1}{2}\) AC (2)
Từ (1) và (2) \(\Rightarrow\) EF // HG và EF = HG
\(\Rightarrow\) Tứ giác EFGH là hình bình hành
Tứ giác EFGH là hình bình hành. EF // AC, EF = \(\frac{1}{2}\) AC
Ta còn có EH là đường trung bình của tam giác ABD
\(\Rightarrow\) EH // BD và EH = \(\frac{1}{2}\) BD
- Tứ giác EFGH là hình chữ nhật
\(\Leftrightarrow\) Hình bình hành EFGH có:
\(\widehat{HEF}=90^o\)
\(\Leftrightarrow HE\perp EF\)
\(\Leftrightarrow EH\perp AC\)
\(\Leftrightarrow AC\perp BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc với nhau thì tứ giác EFGH là hình chữ nhật
- Tứ giác EFGH là hình thoi
\(\Leftrightarrow\) Hình bình hành EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD bằng nhau thì tứ giác EFGH là hình thoi
- Tứ giác EFGH là hình vuông
\(\Leftrightarrow\) Hình chữ nhật EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc và bằng nhau thì tứ giác EFGH là hình vuông