Chọn B.
- Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
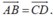
- Với mọi điểm O bất kì khác A, B, C, D ta có:
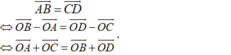
Chọn B.
- Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
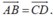
- Với mọi điểm O bất kì khác A, B, C, D ta có:
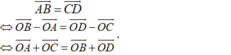
Trong không gian cho điểm O bất kì và bốn điểm A, B, C, D không thẳng hàng. Chứng minh điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: O A → + O C → = O B → + O D →
Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là:
O A → + O C → = O B → + O D →
Cho hình chóp tứ giác S.ABCD. Gọi O là giao điểm AC và BD. Trong các mặt phẳng sau, điểm O nằm trên mặt phẳng nào ?
A.(SAC)
B.(SAB)
C.(SAD)
D.(SBC)
1. Cho hình bình hành ABCD có tâm O, Gọi M, N lần lượt là trung điểm của AB, AO.
a) XĐ ảnh của tam giác AND qua phép tịnh tiến \(\overrightarrow{OC}\)
b)XĐ ảnh của tam giác AMN qua phép vị tự tâm O, tỉ số -2
2. trong mặt phẳng Oxy cho điểm M(1;-5),\(\overrightarrow{v}=\left(-2,1\right)\)đường thẳng d: x-4y+3=0,
đường tròn \(\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=5\)
a) tìm tọa độ M' là ảnh của M qua phép tịnh tiến vecto \(\overrightarrow{v}\)
b)Viết phương trình d' là ảnh của d qua phép quay tâm O, góc quay \(^{-90^o}\)
c) tìm phương trình (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số 2.
3.
Cho đường thẳng (d): x-5y-4=0. Viết phương trình đường thẳng (d') ảnh của (d) qua phép vị tự tâm O , góc 90o và phép vị tự tâm I(-2,3) tỉ số -3
Cho hình chóp S.ABCD có ABCD là tứ giác lồi. Gọi O là giao điểm của AC và BD. Gọi c là giao tuyến các(SAC) và (SBD). Tìm c ?
A. c = SA . B. c = AC. C. c = BD. D. c = SO.
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
2 đường thẳng a và b cắt nhau tại điểm O. Trên a, lấy 8 điểm khác nhau (không tính O), trên b lấy 10 điểm khác nhau (không tính O). Tính số tam giác có 3 đỉnh được lấy từ 19 điểm gồm 18 điểm nêu trên và điểm O.
Đồ thị hàm số y = x 4 - 2 m 2 x 2 + m 2 (m là tham số) có ba điểm cực trị A, B, C sao cho bốn điểm A, B, C, O là bốn đỉnh của hình thoi (O là gốc toạ độ) khi và chỉ khi
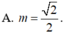
![]()
![]()
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ