Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
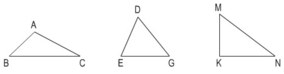
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây: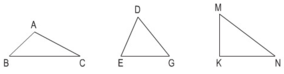
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC ở M. Kẻ MD vuông góc BC
a)C/M BA=BD
b)Gọi E là giao điểm của DM và BA. C/M tâm giác ABC =tam giác DBE
c)Kẻ DH vuông góc MC (H vuông góc MC) và AK vuông góc ME (K vuông góc ME). Gọi N là giao điểm của DH và AK. C/M MN là tia phân giác góc HMK.
d)C/M B,M,N thẳng hàng.
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
=>BA=BD và MA=MD
b: Xét ΔBDE vuông tại D và ΔBAC vuông tại A có
BD=BA
\(\widehat{DBE}\) chung
Do đó: ΔBDE=ΔBAC
c: Xét ΔMKA vuông tại K và ΔMHD vuông tại H có
MA=MD
\(\widehat{KMA}=\widehat{HMD}\)
Do đó: ΔMKA=ΔMHD
=>MK=MH và AK=HD
Xét ΔNKM vuông tại K và ΔNHM vuông tại H có
NM chung
MK=MH
Do đó: ΔNKM=ΔNHM
=>NK=NH và \(\widehat{KMN}=\widehat{HMN}\)
=>MN là phân giác của góc HMK
d: NK+KA=NA
NH+HD=ND
mà NK=NH và KA=HD
nên NA=ND
=>N nằm trên đường trung trực của AD(1)
MA=MD
=>M nằm trên đường trung trực của AD(2)
BA=BD
=>B nằm trên đường trung trực của AD(3)
Từ (1),(2),(3) suy ra B,M,N thẳng hàng
Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi :
a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư
b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó
c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông
d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh
Theo định nghĩa ta thấy kết quả:
a) HÌnh trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.
c) Khối nón tròn xoay.
d) Khối trụ tròn xoay.
Cho hai tam giác bằng nhau: tam giác ABC (không có hai góc nào hoặc hai cạnh nào bằng nhau) và một tam giác có ba đỉnh là I, J, K. Viết kí hiệu về sự bằng nhau của hai tam giác đó, biết rằng:
a) A B = J I , C ^ = K ^
b) AB = IK, AC = IJ.
c) A ^ = K , ^ B ^ = J ^
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ M D ⊥ B C ( D ∈ B C ) .
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ∆ A B C = ∆ D B E .
c) Kẻ D H ⊥ M C ( H ∈ M C ) và A K ⊥ M E ( K ∈ M E ) . Gọi N là giao điểm của hai tia DH và AK. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
ho tam giác ABC vuông ở A có góc C=30 độ . Trên cạnh AB lấy M sao cho góc BCM =2/3 góc ACB, trên cạnh AC lấy N sao cho góc CBN=2/3 góc ABC. Gọi giao của CM và BN là K.
a, Tính góc CKN
b, Gọi F và I lần lượt là hình chiếu của K trên BC và AC, trên tia đối của tia IK lấy D sao cho IK=ID, trên tia KF lấy e sao cho KF=FE( E khác K) . C/m DE=EC=CD
c, C/m ba điểm E,N,D thẳng hàng
Mình làm câu c thôi ( câu a,b mấy trang khác có nha). Hình mn tự vẽ nha.
Theo b, có: Tam giác DCE là tam giác đều
=> DCE=CDE=DEC=60
Xét tam giác CND:
Áp dụng định lí:" Tổng ba góc một tam giác bằng 180"
=>CND+CDN+DCN=180
=>CND+60+10=180 (vì ICD=10; CDE= 60)
=>CND=180-70=110 (1)
Xét tam giác CNE:
Áp dụng định lí:"Tổng ba góc một tam giác bằng 180"
=>CNE+CEN+NCE=180
=>CNE+60+(ACB+ECF)=180
=>CNE+60+30+20=180
=>CNE+110=180
=>CNE=70 (2)
Từ (1) và (2) suy ra: CND+CNE=70+110=180
=>DNE=180 =>DNE là góc bẹt
=>D; N; E thẳng hàng (ĐPCM)
Cho hai tam giác bằng nhau: tam giác ABC (không có hai góc nào hoặc hai cạnh nào bằng nhau) và một tam giác có ba đình I, J, K. Viết kí hiệu về sự bằng nhau của hai tam giác đó biết rằng:
a) AB = JI, C = K
b) AB = IK, AC = IJ
c) A = K, B = J
Ở hình vẽ dưới đây có 3 điểm và 3 đường thẳng nhưng chưa rõ tên của chúng. Biết tên của các điểm ấy là A, B, C còn tên của 3 đường thẳng trong hình là a, b, c
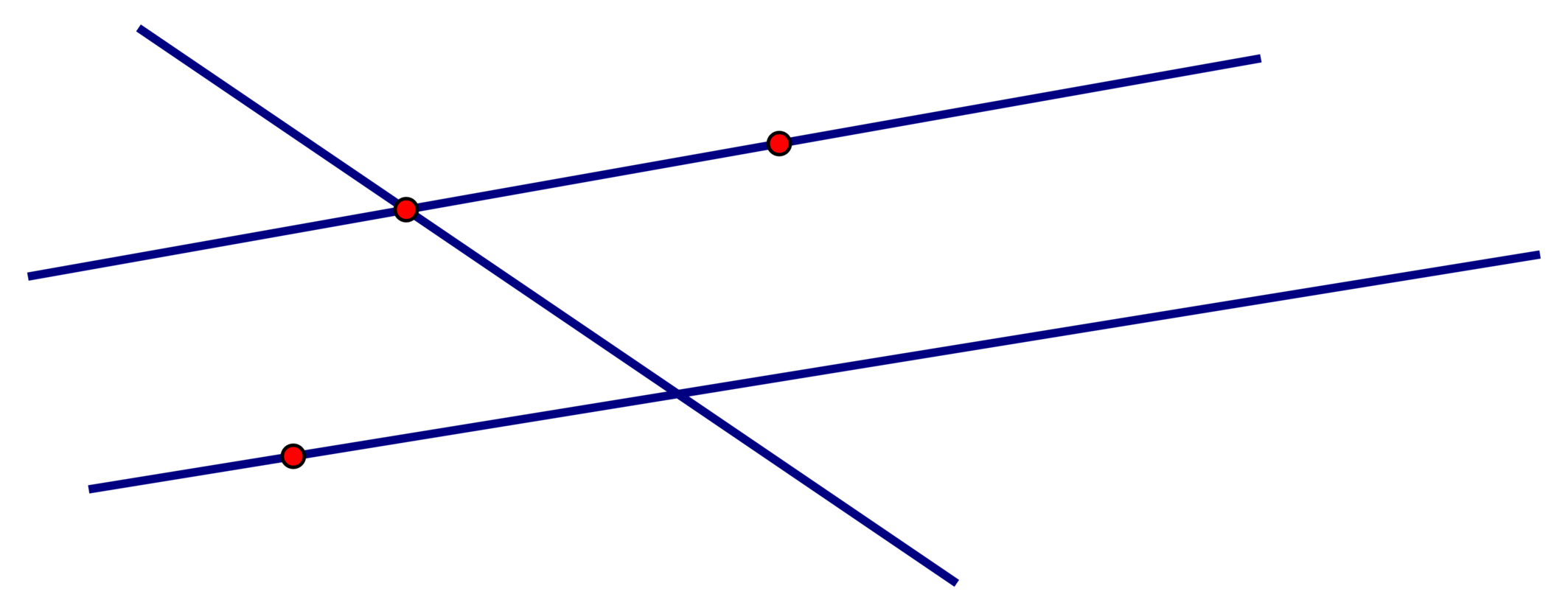
a) Hãy cho biết tên của mỗi điểm và mỗi đường thẳng trong hình, biết rằng A ∈ a , B ∈ b , C ∈ c và A ∈ b
b) Hãy tìm điểm thứ tư (khác với ba điểm trên) và đặt tên cho điểm đó. Biết rằng đó là điểm chung của đường thẳng b và c.
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại D.
a) Cho biết góc ACB = 40 độ. Tính số đo góc ABD
b) Trên cạnh BC lấy điểm E sao cho BE=BA. Chứng minh tam giác BAD = tam giác BED và DE vuông góc với BC
c) Gọi F là giao điểm của BA và ED. Chứng minh rằng tam giác ABC = tam giác EBF
d) Vẽ CK vuông góc với BD tại K. Chứng minh ba điểm K ,F ,C thẳng hàng
Help mk vs nha!!! ^^