Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,  A B C ^ = 60 ∘ .Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính diện tích  S m c của mặt cầu ngoại tiếp hình chóp S.ABC.

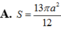
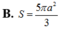
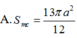
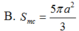
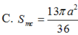
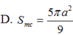
Cho hình chóp S.ABCD  có đáy ABCD là hình thoi cạnh a, ABC =  60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh SB=a 2  . Mệnh đề nào dưới đây sai?

A.  S A B C D = a 2 3 2

B. SC=a 2

C. (SAC ) ⊥ (SBD).

D.    V S . A B C D = 5 3 a 3 12

Cho hình chóp S.ACBD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD),  S A B ^ = 60°, SA = 2a Tính thể tích V của khối chóp S.ABCD

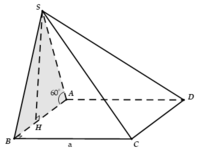
A. V = a 3 3 3

B.  V = a 3 3

C. V = 2 a 3 3 3

D. V = a 3

Cho hình chóp S.ABCD  có đáy ABCD là hình thoi cạnh a,  A B C ^ = 60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh S B = a 2 . Mệnh đề nào dưới đây sai?

A.  S A B C D = a 2 3 2

B.  S C = a 2

C.  S A C ⊥ S B D

D.  V S . A B C D = a 3 3 12

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a ,   A B C ^ = 60 0 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính diện tích S m c  của mặt cầu ngoại tiếp hình chóp S.ABC.

A.  S m c = 13 π a 2 12

B.  S m c = 5 π a 2 3

C.  S m c = 13 π a 2 36

D.  S m c = 5 π a 2 9

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, A B C ^ = 60 ° , mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng

A.  a 6 4

B. a

C.  a 3 2

D.  a 21 7

Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a và S A B ^ = S A D ^ = B A D ^ = 60 °  cạnh bên SA=a. Thể tích khối chóp tính theo a là:

A.  a 3 2 2

B.  a 3 2 3

C.  a 3 2 6

D.  a 3 2 12

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi M và N lần lượt là trung điểm của các cạnh AB, CD. Khoảng cách giữa hai đường thẳng CM và SN bằng

A.  a 3 4

B.  3 a 2 2

C.  a 3 2

D.  3 a 2