Bài 3. Ta có

Mà sinx < 0 ⇔ x ∈ (π + k2π , 2π + k2π), k ∈ Z nên lấy đối xứng qua trục Ox phần đồ thị của hàm số y = sinx trên các khoảng này còn giữ nguyên phần đồ thị hàm số y = sinx trên các đoạn còn lại ta được đồ thị của hàm số y = IsinxI

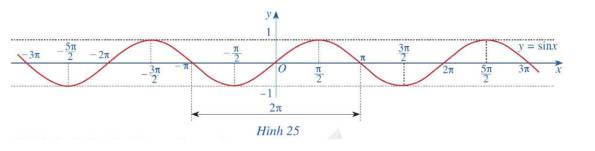
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)

b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.

Như vậy hàm số \(y = \sin x\) là hàm số lẻ.

c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)

Như vậy, hàm số \(y = \sin x\) có tuần hoàn .

d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)

Nhìn đồ thị y = sinx ta thấy trong đoạn [-π ; π] các điểm nằm phía trên trục hoành của đồ thị y = sinx là các điểm có hoành độ thuộc khoảng (0 ; π). Từ đố, tất cả các khoảng giá trị của x để hàm số đó nhận giá trị dương là (0 + k2π ; π + k2π) hay (k2π ; π + k2π) trong đó k là một số nguyên tùy ý.

Đồ thị hàm số y = sin x:

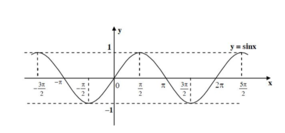
Dựa vào đồ thị hàm số y = sin x ta thấy

y = sin x > 0

⇔ x ∈ (-2π; -π) ∪ (0; π) ∪ (2π; 3π) ∪…

hay x ∈ (k2π; π + k2π) với k ∈ Z.