Hình 3.8 có A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ . Chứng tỏ rằng a // b.
theo giả thiết
\(\angle\left(A1\right)-2\angle\left(A2\right)=\angle\left(B1\right)-2\angle\left(B2\right)\)
\(< =>180-3\angle\left(A2\right)=180-3\angle\left(B2\right)\)
\(< =>-3\angle\left(A2\right)+3\angle\left(B2\right)=0\)
\(< =>-3\left[\angle\left(A2\right)-\angle\left(B2\right)\right]=0\)
điều này xảy ra\(< =>\angle\left(A2\right)=\angle\left(B2\right)\)
2 góc ở vt so le trong \(=>dpcm\)
a,(1/2-2/3)^2
b,2:(1/2-2/3)^2
c,0,25^3.8^3
d,(-12)^4.6^4
e, 2:(1/2-2/3)^2+0,25^3.8^3-(-12)^4.6^4
(mai em thi rồi ạ)
Nếu a=1 \Rightarrow (2008a+3b+1).(2008a+2008a+b)>225(2008a+3b+1).(2008a+2008a+b)>225trái với đề bài
\Rightarrow a=0(vì a là số tự nhiên)
\Rightarrow (2008a+3b+1).(2008a+2008a+b)=(2008.0+3b+1).(20080+2008.0+b)=(3b+1).(b+1)=225(2008a+3b+1).(2008a+2008a+b)=(2008.0+3b+1).(20080+2008.0+b)=(3b+1).(b+1)=225 (1)
Ta có: 225=25.9=(3.8+1).(8+1)225=25.9=(3.8+1).(8+1) (2)
Từ (1) và (2) \Rightarrow b=8
Vậy a=0;b=8
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b,c và giá trị lượng giác của góc A
a) Tính \({a^2}\) theo \(B{D^2}\) và \(C{D^2}\)
b) Tính \({a^2}\) theo b, c và DA.
c) Tính DA theo c và \(\cos A\).
d) Chứng minh \({a^2} = {b^2} + {c^2} - 2bc\;\cos A.\)
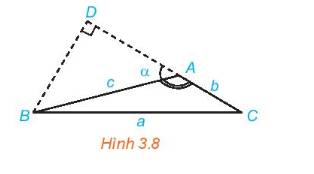
a) Xét tam giác BDC vuông tại D, theo định lý Pythagore ta có:
\({a^2} = B{D^2} + D{C^2}\) (1)
b) Xét tam giác vuông BDA ta có:
\(\left\{ \begin{array}{l}B{A^2} = B{D^2} + D{A^2} \Rightarrow B{D^2} = B{A^2} - D{A^2} = {c^2} - D{A^2}\\\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \end{array} \right.\)
Lại có: DC = DA + AC = DA + b Thế vào (1)
\( \Rightarrow {a^2} = \left( {{c^2} - D{A^2}} \right) + {\left( {DA + b} \right)^2}\) (2)
c) Xét tam giác vuông BDA ta có:
\(\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \)
Mà \(\cos \alpha = - \cos A\) (do góc \(\alpha \) và góc A bù nhau)
\( \Rightarrow DA = - \,\,c.\cos A\)
d) Thế \(DA = - \,\,c.\cos A\) vào (2) ta được:
\(\begin{array}{l}{a^2} = \left[ {{c^2} - {{\left( { - \,\,c.\cos A} \right)}^2}} \right] + {\left( { - \,\,c.\cos A + b} \right)^2}\\ \Leftrightarrow {a^2} = \left( {{c^2} - \,\,{c^2}.{{\cos }^2}A} \right) + \left( {{c^2}.{{\cos }^2}A - \,2b\,c.\cos A + {b^2}} \right)\\ \Leftrightarrow {a^2} = {c^2} - \,\,{c^2}.{\cos ^2}A + {c^2}.{\cos ^2}A - \,2b\,c.\cos A + {b^2}\\ \Leftrightarrow {a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\end{array}\) (đpcm)
1.Rut gọn
a)2^15.9^4/6^3.8^3
b)2^7.9^3/6^5/6^5.8^2
tính lũy thừa : a)(3.8)^3.5/2^9.15^2
giúp mik vs
\(\frac{\left(3.8\right)^3.5}{2^9.15^2}\)
\(=\frac{\left[3.\left(2^3\right)\right]^3.5}{2^9.\left(3.5\right)^2}\)
\(=\frac{3^3.2^9.5}{2^9.3^2.5^2}\)
\(=\frac{3}{5}\)
A = 1/1.3 + 1/3.5 + 1/5.7 + . . . + 1/55.57
b = 1/4 +1/28 + 1/70 + ...+1/58.61
c = 2/ 3.8 + 2/8.13 + 2/13.18 + . . . + 2/498.503
~chọn 1 trong 3 câu để làm ạ~
3 câu như nhau cả thôi :v
\(A=\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+...+\frac{1}{55\cdot57}\)
\(A=\frac{1}{2}\left(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+\frac{2}{5\cdot7}+...+\frac{2}{55\cdot57}\right)\)
\(A=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{55}-\frac{1}{57}\right)\)
\(A=\frac{1}{2}\left(1-\frac{1}{57}\right)\)
\(A=\frac{1}{2}\cdot\frac{56}{57}\)
\(A=\frac{28}{57}\)
a,5/3-2/3.x=1
b.4/5+5/7:x=1/6
c,1/8.x+4/3.8/7=2/4x.3/4
\(a,\frac{5}{3}-\frac{2}{3}.x=1\)
\(\frac{5}{3}-1=\frac{2}{3}.x\)
\(\frac{2}{3}=\frac{2}{3}.x\)
\(x=\frac{2}{3}:\frac{2}{3}\)
\(x=1\)
\(b,\frac{4}{5}+\frac{5}{7}.x=\frac{1}{6}\)
\(\frac{5}{7}.x=\frac{1}{6}-\frac{4}{5}\)
\(\frac{5}{7}.x=-\frac{19}{30}\)
\(x=-\frac{19}{30}:\frac{5}{7}\)
\(x=-\frac{133}{150}\)
A = ( 156.2 + 3.8 -17.5 + 252.5 - 197 ) x ( 0.2 - 2 / 10 ) x 2001
