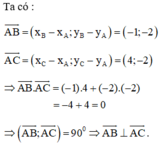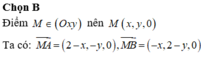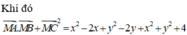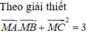Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.

Những câu hỏi liên quan
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho
M
A
2
−
2
M
B
2
lớn nhất. A.
M
0
;
0
;
5
.
B.
M...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 − 2 M B 2 lớn nhất.
A. M 0 ; 0 ; 5 .
B. M 1 2 ; − 3 2 ; 0 .
C. M 3 ; − 4 ; 0 .
D. M 3 2 ; 1 2 ; 0 .
Đáp án C
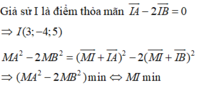
Suy ra M là hình chiếu vuông góc của I lên (Oxy) => I(3;-4;0)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho
M
A
2
-
2
M
B
2
lớn nhất. A.
M
0
;
0
;
5
B.
M
1
2...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A. M 0 ; 0 ; 5
B. M 1 2 ; - 3 2 ; 0
C. M 3 ; - 4 ; 0
D. M 3 2 ; 1 2 ; 0
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho
M
A
2
-
2
M
B
2
lớn nhất.
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
![]()
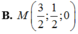
![]()
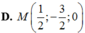
Đáp án A.
Cách giải:
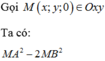
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Chứng minh AB→ ⊥ AC→.
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho
M
A
2
-
2
M
B
2
lớn nhất.
A
.
M
3
2
;
1
2
;
0...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A . M 3 2 ; 1 2 ; 0
B . M 1 2 ; - 3 2 ; 0
C. M (0; 0; 5)
D. M (3; -4; 0)
Trong không gian Oxyz,cho điểm A(1;2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oxy) là điểm
A. N(1;2;0)
B. M(0;0;3)
C. P(1;0;0)
D. Q(0;2;0)
Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M ( x 0 ; y 0 ; z 0 ) trên mặt phẳng (Oxy) là điểm M ' ( x 0 ; y 0 ; z 0 )
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)
Đúng 0
Bình luận (0)
Trong không gian Oxyz,cho điểm A(1;2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oxy) là điểm
A. N(1;2;0)
B. M(0;0;3)
C. P(1;0;0)
D. Q(0;2;0)
Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M(x0;y0;z0) trên mặt phẳng (Oxy) là điểm M’(x0;y0;z0)
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)
Đúng 0
Bình luận (0)
Cho A(2;0;0), B(0;2;0), C(0;0;2). Tập hợp các điểm M trên mặt phẳng (Oxy) sao cho
M
A
→
.
M
B
→
+
M
C
→
2
3
là
Đọc tiếp
Cho A(2;0;0), B(0;2;0), C(0;0;2). Tập hợp các điểm M trên mặt phẳng (Oxy) sao cho M A → . M B → + M C → 2 = 3 là
![]()
![]()
![]()
![]()
Cho A(2;0;0), B(0;2;0), C(0;0;2). Tập hợp các điểm M trên mặt phẳng (Oxy) sao cho
M
A
→
.
M
B
→
+
M
C
→
2
3
là A. Một đường elip B. Một đường tròn C. Một đường thẳng D. Một mặt cầu
Đọc tiếp
Cho A(2;0;0), B(0;2;0), C(0;0;2). Tập hợp các điểm M trên mặt phẳng (Oxy) sao cho M A → . M B → + M C → 2 = 3 là
A. Một đường elip
B. Một đường tròn
C. Một đường thẳng
D. Một mặt cầu
Cho điểm M ( 1 ; 2 ; - 3 ) , hình chiếu vuông góc của điểm M trên mặt phẳng (Oxy) là:
A. M'(1;2;0)
B. M'(1;0;-3)
C. M'(0;2;-3)
D. M'(1;2;3)
Chọn A.
Với M (a,b,c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M1(a;b;0)
Do đó, hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).
Đúng 0
Bình luận (0)